Paths on a Grid POJ - 1942 排列组合

题意：

从左下角移动到右上角。每次只能向上或者向右移动一格。问移动的轨迹形成的右半边图形有多少种

题解：

注意，这个图形就根本不会重复，那就是n*m的图形，向上移动n次，向右移动m次。

从左下角移动到右上角的过程就是n个“上”，m个“右”的组合的形式，有多少种移动方式，那就是 C((n+m),n)或者C((n+m),m) C((n+m),n)意思就是从n+m个位置上挑选出来n个位置，这n个位置要向上走，那么剩下m个位置肯定是向右走咯

另外 无符号整型的输入输出用“%u” 无符号长整型的输入输出用“%llu”

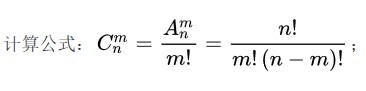
本题的N=(n+m),M=min(n,m)

将N，M带入公式，你会发现N！与(N-M)!（N-M是max(n,m)）约分后剩下的是N*(N-1)*(N-2)*...（一共m个元素）

代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<math.h>
 6 #include<queue>
 7 using namespace std;
 8 typedef unsigned ull;
 9 ull result(ull n,ull m) //求组合C（n，m）（n>m）
10 {
11     ull temp;
12     double ans=1.0;
13     temp=min(n,m);
14     n=n+m;
15     m=temp;
16     while(m>0)
17     {
18         ans=ans*((double)(n--)/(double)(m--));
19     }
20     ans+=0.5;
21     return (ull)ans;
22 }
23 int main()
24 {
25     unsigned m,n;
26     while(true)
27     {
28         scanf("%u%u",&n,&m);
29         if(!m && !n)//承认这题的猥琐吧！竟然有其中一边为0的矩阵，一定要&&，用||会WA
30             break;
31         printf("%u\n",result(n,m));
32         //cout<<<<endl;
33     }
34     return 0;
35 }