支持向量机SVM介绍

SVM为了达到更好的泛化效果，会构建具有"max-margin"的分类器（如下图所示），即最大化所有类里面距离超平面最近的点到超平面的距离，数学公式表示为$$\max\limits_{\vec{w},b}Margin(\vec{w},b)=\max\limits_{\vec{w},b}\min\limits_{i=1,2,\cdots,n}\frac{1}{\lVert{\vec{w}}\rVert_2}y_i(\vec{w}\cdot\vec{x}_i+b),\text{ }y_i\in\{-1,1\}$$

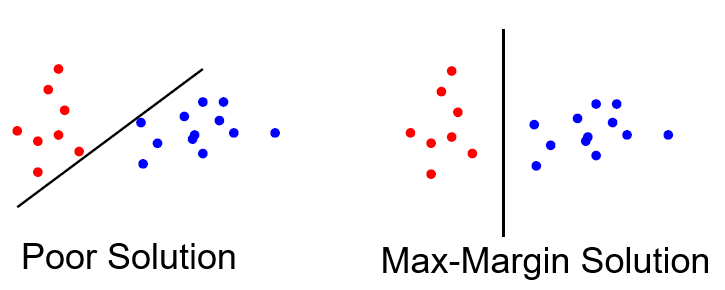
Linear SVM

上述公式可以改写为如下形式$$\min\limits_{\vec{w},b}\frac{1}{2}\lVert{\vec{w}}\rVert_2^2,\text{ subject to } y_i(\vec{w}\cdot\vec{x}_i+b)\geq{1} \text{ for all }i$$

这是一个典型的二次规划问题，并且仅当两个类是线性可分时才有解。可以使用拉格朗日乘数法进行求解，定义$$L(\vec{w},b,\alpha_1,\cdots,\alpha_n)=\frac{1}{2}\lVert{\vec{w}}\rVert_2^2+\sum_{i=1}^n\alpha_i[1-y_i(\vec{w}\cdot\vec{x}_i+b)]$$则SVM的求解问题转换为$\min\limits_{\vec{w},b}[\max\limits_{\alpha_1,\cdots,\alpha_n\geq{0}}L(\vec{w},b,\alpha_1,\cdots,\alpha_n)]$，基于SVM问题的强对偶性，下列等式成立：$$\min\limits_{\vec{w},b}[\max\limits_{\alpha_1,\cdots,\alpha_n\geq{0}}L(\vec{w},b,\alpha_1,\cdots,\alpha_n)]=\max\limits_{\alpha_1,\cdots,\alpha_n\geq{0}}[\min\limits_{\vec{w},b}L(\vec{w},b,\alpha_1,\cdots,\alpha_n)]$$针对上式等号右边的极值问题，首先有$$\frac{\partial{L}}{\partial{\vec{w}}}=0 \Rightarrow \vec{w}=\sum_{i=1}^n\alpha_iy_i\vec{x}_i \text{, }\frac{\partial{L}}{\partial{b}}=0 \Rightarrow \sum_{i=1}^ny_i\alpha_i=0$$将结果带入$L$中可以得到SVM的对偶形式：$$\max\limits_{\alpha_1,\cdots,\alpha_n\geq{0},\sum_{i=1}^ny_i\alpha_i=0}(\sum\limits_{i=1}^n\alpha_i-\frac{1}{2}\sum\limits_{i=1}^n\sum\limits_{j=1}^n\alpha_i\alpha_jy_iy_j\vec{x}_i\cdot\vec{x}_j)$$针对$b$的求解，可以利用KKT条件：$\alpha_i[1-y_i(\vec{w}\cdot\vec{x}_i+b)]=0\text{ for }i=1,2,\cdots,n$，即取任一不为0的$\alpha_i$，令$1-y_i(\vec{w}\cdot\vec{x}_i+b)=0$

最终求得的分类器为$g_{svm}(\vec{x})=sign(\vec{w}\cdot\vec{x}+b)\text{, with }\vec{w}=\sum_{i=1}^n\alpha_iy_i\vec{x}_i$

Kernel SVM

上述的Linear SVM为线性分类器，因此引入核的概念扩展原始数据的维数，使其可以在原始数据空间上变为非线性分类器。核函数的优点是相比于直接进行特征映射可以很大程度上减少计算量，并且维数的扩展形式更加灵活，具体做法是将Linear SVM的对偶形式中两个数据向量的相乘变为核函数的形式，即$$\max\limits_{\alpha_1,\cdots,\alpha_n\geq{0},\sum_{i=1}^ny_i\alpha_i=0}[\sum\limits_{i=1}^n\alpha_i-\frac{1}{2}\sum\limits_{i=1}^n\sum\limits_{j=1}^n\alpha_i\alpha_jy_iy_jK(\vec{x}_i,\vec{x}_j)]$$核函数$K$需要满足以下性质：定义核函数矩阵$K$（$K$中的元素$K_{ij}=K(\vec{x}_i,\vec{x}_j)$），则矩阵$K$需为半正定对称矩阵。常用的核函数主要有以下两种：

多项式核函数$K(\vec{x}_i,\vec{x}_j)=(r\vec{x}_i\cdot\vec{x}_j+\epsilon)^d\text{, with }r>0,d\text{ is positive integer},\epsilon\geq{0}$
高斯核函数$K(\vec{x}_i,\vec{x}_j)=e^{-\gamma\lVert\vec{x}_i-\vec{x}_j\rVert_2^2}\text{, with }\gamma>0$

针对$b$的求解，仍利用KKT条件，取任一不为0的$\alpha_i$，令$1-y_i(\sum_{k=1}^n\alpha_ky_kK(\vec{x}_k,\vec{x}_i)+b)=0$

最终求得的分类器为$g_{svm}(\vec{x})=sign(\sum_{i=1}^n\alpha_iy_iK(\vec{x}_i,\vec{x})+b)$

Soft-Margin SVM

Linear SVM仅当数据为线性可分时才有解，这就使得其实际应用有很大的限制，因此对它的原始公式进行一定程度的改进，使其对错误分类有一定程度的容忍度，具体公式如下：$$\min\limits_{\vec{w},b}(\frac{1}{2}\lVert{\vec{w}}\rVert_2^2+C\sum\limits_{i=1}^n\epsilon_i),\text{ subject to } y_i(\vec{w}\cdot\vec{x}_i+b)\geq{1-\epsilon_i},\epsilon_i\geq{0} \text{ for all }i$$上式中的C越小，对错误分类的容忍度就越高；当C趋于无穷大时就变为了Linear SVM的形式。仍使用拉格朗日乘数法以及SVM的强对偶性质，定义$$L(\vec{w},b,\epsilon_i,\alpha_i,\mu_i)=\frac{1}{2}\lVert{\vec{w}}\rVert_2^2+C\sum\limits_{i=1}^n\epsilon_i+\sum_{i=1}^n\alpha_i[1-\epsilon_i-y_i(\vec{w}\cdot\vec{x}_i+b)]-\sum\limits_{i=1}^n\mu_i\epsilon_i$$上式可变为求解$$\min\limits_{\vec{w},b,\epsilon_i}[\max\limits_{\alpha_i,\mu_i\geq{0}}L(\vec{w},b,\epsilon_i,\alpha_i,\mu_i)]=\max\limits_{\alpha_i,\mu_i\geq{0}}[\min\limits_{\vec{w},b,\epsilon_i}L(\vec{w},b,\epsilon_i,\alpha_i,\mu_i)]$$同样令$\frac{\partial{L}}{\partial{\vec{w}}}=\frac{\partial{L}}{\partial{b}}=\frac{\partial{L}}{\partial{\epsilon_i}}=0$，则对偶问题可写为$$\max\limits_{0\leq\alpha_i\leq{C},\sum_{i=1}^ny_i\alpha_i=0}(\sum\limits_{i=1}^n\alpha_i-\frac{1}{2}\sum\limits_{i=1}^n\sum\limits_{j=1}^n\alpha_i\alpha_jy_iy_j\vec{x}_i\cdot\vec{x}_j)$$同样可以将$\vec{x}_i\cdot\vec{x}_j$替换为$K(\vec{x}_i,\vec{x}_j)$，在分类器中引入核函数，上述对偶问题的KKT条件为:$$\begin{cases} \alpha_i=0:\text{ the point away from the margin boundary with }\epsilon_i=0 \\ 0<\alpha_i<C:\text{ the point on the margin boundary with }\epsilon_i=0\text{ and }1-y_i(\sum_{k=1}^n\alpha_ky_kK(\vec{x}_k,\vec{x}_i)+b)=0 \\ \alpha_i=C:\text{ the point violate the margin boundary with }\epsilon_i>0(\text{the violate amount}) \end{cases}$$

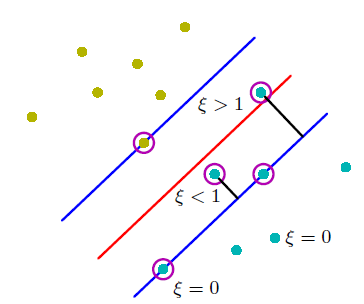
最终求得的分类器为$g_{svm}(\vec{x})=sign(\sum_{i=1}^n\alpha_iy_iK(\vec{x}_i,\vec{x})+b)$

Unconstraint Soft-Margin and SVR

Soft-Margin SVM还可以改写成以下形式：$$\min\limits_{\vec{w},b}[\underbrace{\frac{1}{2C}\lVert{\vec{w}}\rVert_2^2}_\text{Regularization Term}+\sum\limits_{i=1}^n\underbrace{\max(1-y_i(\vec{w}\cdot\vec{x}_i+b),0)}_\text{Loss Function}]$$若在训练中对每个样本分配不同的权重，则上式变为$$\min\limits_{\vec{w},b}[\frac{1}{2C}\lVert{\vec{w}}\rVert_2^2+\sum\limits_{i=1}^ns_i\max(1-y_i(\vec{w}\cdot\vec{x}_i+b),0)]$$求解过程与不加权重的Soft-Margin SVM是一致的，只不过需要将$0\leq\alpha_i\leq{C}$变为$0\leq\alpha_i\leq{Cs_i}$

受上述形式的启发，支持向量机也可用于回归问题（SVR），定义$\epsilon\text{-insensitive loss function }err(y,\hat{y})=\max(\lvert{y-\hat{y}}\rvert-\epsilon,0)$，则SVR为L2正则化的回归问题：$$\min\limits_{\vec{w},b}[\sum\limits_{i=1}^nerr(y_i,\hat{y}_i)+\frac{1}{2C}\lVert{\vec{w}}\rVert_2^2]=\min\limits_{\vec{w},b}[\sum\limits_{i=1}^n\max(\lvert{y_i-(\vec{w}\cdot\vec{x}_i+b)}\rvert-\epsilon,0)+\frac{1}{2C}\lVert{\vec{w}}\rVert_2^2]$$具体求解思路和Soft-Margin SVM基本相同，这里就不再详细叙述了。