洛谷 P4408 [NOI2003]逃学的小孩

题目描述

Chris家的电话铃响起了，里面传出了Chris的老师焦急的声音：“喂，是Chris的家长吗？你们的孩子又没来上课，不想参加考试了吗？”一听说要考试，Chris的父母就心急如焚，他们决定在尽量短的时间内找到Chris。他们告诉Chris的老师：“根据以往的经验，Chris现在必然躲在朋友Shermie或Yashiro家里偷玩《拳皇》游戏。现在，我们就从家出发去找Chris，一但找到，我们立刻给您打电话。”说完砰的一声把电话挂了。

Chris居住的城市由N个居住点和若干条连接居住点的双向街道组成，经过街道x需花费Tx分钟。可以保证，任两个居住点间有且仅有一条通路。Chris家在点C，Shermie和Yashiro分别住在点A和点B。Chris的老师和Chris的父母都有城市地图，但Chris的父母知道点A、B、C的具体位置而Chris的老师不知。

为了尽快找到Chris，Chris的父母会遵守以下两条规则：

如果A距离C比B距离C近，那么Chris的父母先去Shermie家寻找Chris，如果找不到，Chris的父母再去Yashiro家；反之亦然。
Chris的父母总沿着两点间唯一的通路行走。

显然，Chris的老师知道Chris的父母在寻找Chris的过程中会遵守以上两条规则，但由于他并不知道A，B，C的具体位置，所以现在他希望你告诉他，最坏情况下Chris的父母要耗费多长时间才能找到Chris？

输入格式

输入文件第一行是两个整数N（3 ≤ N ≤ 200000）和M，分别表示居住点总数和街道总数。

以下M行，每行给出一条街道的信息。第i+1行包含整数Ui、Vi、Ti（1≤Ui, Vi ≤ N，1 ≤ Ti ≤ 1000000000），表示街道i连接居住点Ui和Vi，并且经过街道i需花费Ti分钟。街道信息不会重复给出。

输出格式

输出文件仅包含整数T，即最坏情况下Chris的父母需要花费T分钟才能找到Chris。

输入输出样例

输入样例

输出样例

分析

我们要从点C出发先走到点A再走到点B(CA<CB) 或者是从点C出发先走到点B再走到点A(CB<CA)

其实这两种情况是一样的，因为A、B的位置我们不确定，所以两点可以互换，所以我们把题目简化：

一句话题意：在一棵树上找三个点A、B、C使得AB+AC的值最大（满足AC<=BC）

这道题可以说是一个模板题，虽然题目中又是逃学又是找人，但实际上是让你求树的直径

AB的最大值很好想，显然就是树的直径，在一棵树中没有比直径更长的路程了

那么AC的最大值呢，我们可以在dfs求树的直径的时候顺便把每一个点到A、B的价值都求出来，在这两个价值中取较小值（因为要先到比较近的点）

最后再枚举一遍求最优决策（最大值），这实际上是一种贪心的思想

我们引用一下洛谷上的证明：传送门

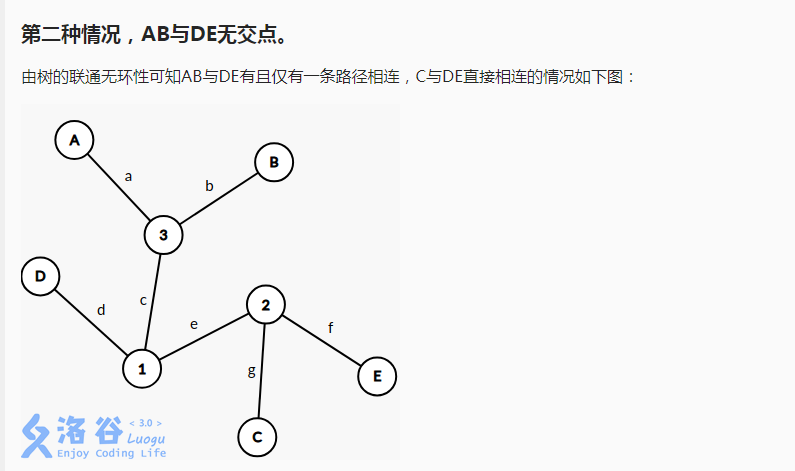
最后要注意几个细节：

1、开long long，并且赋值为无穷大时要写8个3f：0x3f3f3f3f3f3f3f3f

2、双向边，开数组时一定要乘2

3、数组不能开得太大

这三个细节我每个都错了一遍

代码

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const int maxn=;//数组不要开小了
 typedef long long ll;//记得开long long
 struct asd{
     ll from,to,next,val;
 }b[maxn];
 ll n,m;
 ll head[maxn],tot=;
 void ad(ll aa,ll bb,ll cc){
     b[tot].from=aa;
     b[tot].to=bb;
     b[tot].next=head[aa];
     b[tot].val=cc;
     head[aa]=tot++;
 }//加边函数
 ll dis[maxn],disA[maxn],disB[maxn],A,B;
 //disA是每个点到端点A的距离,disB是，每个点到端点B的距离
 //A、B为端点A、B的编号
 ll zhijing,jl=-0x3f3f3f3f3f3f3f3f,id=;//定义直径
 void dfs(ll now,ll fa){
     for(ll i=head[now];i!=-;i=b[i].next){
         ll u=b[i].to;
         ll da=b[i].val;
         if(u==fa) continue;
         dis[u]=dis[now]+da;
         if(dis[u]>jl){
             jl=dis[u];
             id=u;
         }
         dfs(u,now);
     }
 }//dfs求直径
 int main() {
     scanf("%lld%lld",&n,&m);
     memset(head,-,sizeof(head));
     for(ll i=;i<=m;i++){
         ll aa,bb,cc;
         scanf("%lld%lld%lld",&aa,&bb,&cc);
         ad(aa,bb,cc);
         ad(bb,aa,cc);
     }
     dfs(,);//第一遍dfs求A点标号
     A=id;
     memset(dis,,sizeof(dis));
     id=,jl=-0x3f3f3f3f3f3f3f3f;
     dfs(A,);//第二遍dfs求B点标号以及每一个点到A点的距离
     B=id,zhijing=jl;
     id=,jl=-0x3f3f3f3f3f3f3f3f;
     for(ll i=;i<=n;i++){
         disA[i]=dis[i];
     }
     memset(dis,,sizeof(dis));
     dfs(B,);//第三遍dfs求每一个点到B点的距离，每次dfs之前不要忘了初始化
     for(ll i=;i<=n;i++){
         disB[i]=dis[i];
     }
     ll ans=-0x3f3f3f3f3f3f3f3f;
     for(ll i=;i<=n;i++){
         ans=max(ans,min(disA[i],disB[i]));
     }//求最最优决策
     printf("%lld\n",ans+zhijing);//输出
     return ;
 }