6.29模拟赛 （T1:李时珍的皮肤衣 T2:马大嘴的废话 T3:SSY的队列 T4:清理牛棚);

啊，又是考炸的一天，成功的退步了三名，啊，成共的看错了T1  的题意 ，水了80分。

第十五名就是我，额，已经有点倒数的感觉了，并且一道题都没AC  我太难了。

好了，废话不多说了，下面正式提接：

这到题呵呵，很水吧，不想多说，自己找规律吧，直接吧代码给你们：（不要问我为什么写挂了，（没看清提））

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll  long long
ll n;
ll Pow(ll a,ll b){
    ll ans = 1;
    ll base = a;
    while(b){
        if((b & 1) !=0){
            ans = (ans*base)%n;
        }
        base = (base*base)%n;
        b>>=1;
    }
    return ans;
}
int main(){
	std::ios::sync_with_stdio(false);

	cin>>n;
	ll ans = Pow(2,n-1);
	ll jl = (ans+1)%n;
	cout<<jl<<endl;
}

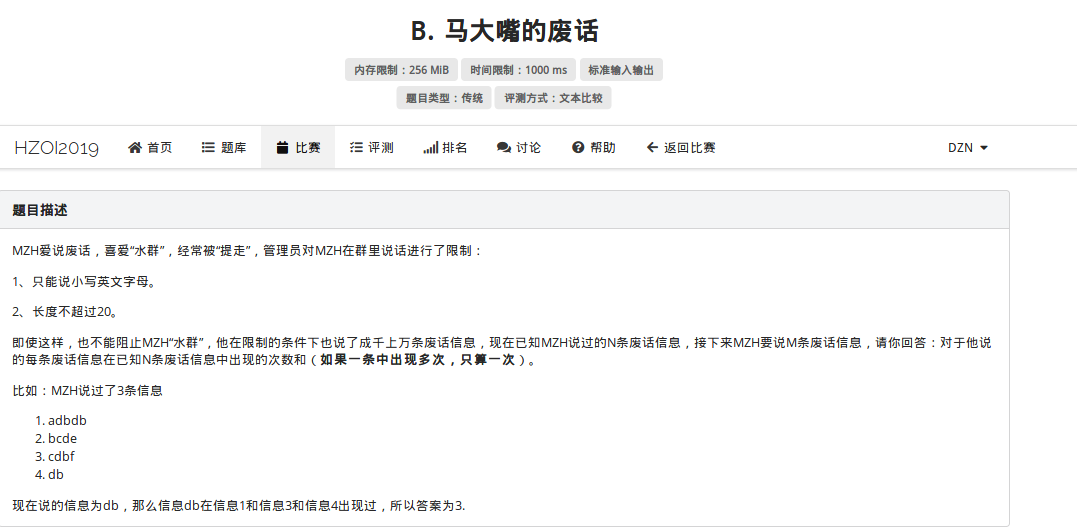
这道题就很有意思了，显然的暴力60pts

但是正解真么办呢？

如果学过AC自动机的很快就会发现就是一个板子，但是我没学过呀，怎么办？

那么我们就要把tire树请上场了，如果不懂的话给你推荐个博客。链接

然后显然的你已经懂了，直接看代码吧：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=5e5+10;
int tire[maxn][26],mark[maxn][26],cnt[maxn][26];
int n,m;
int tot=0;
char s[30];
char a[30];
void insert(int l,int r,int id){//id :防止反复插入
	int now=0;
	int t;
	for(int i=l;i<=r;i++){
		t=s[i]-'a';
		if(tire[now][t]){
			if(id!=mark[now][t]){
			cnt[now][t]++;
			mark[now][t]=id;
			}
		}
		else {
			tire[now][t]=++tot;
			mark[now][t]=id;
			cnt[now][t]=1;
		}
		now=tire[now][t];
	}
}
int query(char a[]){
	int len=strlen(a);
	int now=0,ans=0;
	for(int i=0;i<len;i++){
		int t=a[i]-'a';
		if(tire[now][t]==0)return 0;
		ans=cnt[now][t];
		now=tire[now][t];
	}
	return ans;
}
int main(){
	//freopen("a.in","r",stdin);
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>s;
		int len=strlen(s);
		for(int j=0;j<len;j++){//插入方式，把它的子串加进去
			insert(j,len-1,i);
		}
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>a;
		cout<<query(a)<<'\n';//直接查寻走人
	}
	return 0;
}

OK ,

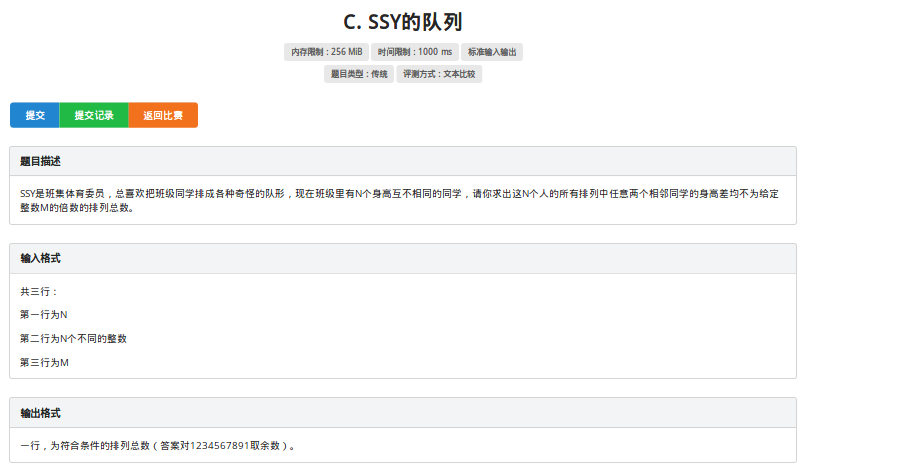
啊，一看这题就知道不再我能力范围内，但是一看数据范围，用状压DP 可以水70分。

正解是 hash 但是我不会，所以我把Dp的代码献给你们吧！

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int Mod,n,a[50];ll M=1234567891,dp[1<<22][31];
int main(){
	scanf("%d",&n);for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	scanf("%d",&Mod);int ed=(1<<n)-1;
	for(int i=1;i<=n;++i) dp[1<<(i-1)][i]=1;
	for(int j=0;j<=ed;++j)
		for(int i=1;i<=n;++i)
			for(int k=1;k<=n;++k){
				if((i==k)||(!(j & (1<<(k-1))))||(j & (1<<(i-1)))||(abs(a[k]-a[i])%Mod==0)) continue;
				dp[j|(1<<(i-1))][i]=(dp[j|(1<<(i-1))][i]+dp[j][k]) % M;
			}
	ll ans=0;for(int i=1;i<=n;++i) ans=(ans+dp[ed][i])%M;
	printf("%lld\n",ans);
	return 0;
}

代码很短，重构代码过的。

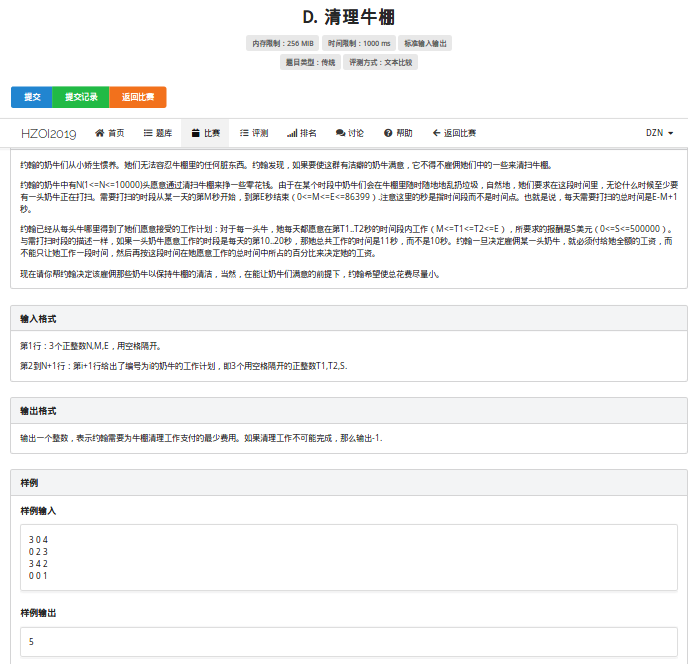
这题一看，首想区间DP 复杂度 O(n^3)只能拿 20 分。

然后想到了线性DP  O(n^2)。

然后居然水过了。（数据太水了）;

代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1e4+5,M=1e6+5;
int n, s, t;
struct node {
	int l, r, w;
} e[N];
bool cmp ( node a, node b){
	if(a.l == b.l) return a.r < b.r;
	else return a.l < b.l;
}
int f[M];
int main(){
	//freopen ("a.in", "r", stdin);
	std::ios::sync_with_stdio( false );
	std::cin.tie( 0 );
	cin>> n >> s >> t;
	for(int i = 1; i <= n; i++){
		cin>> e[i].l >> e[i].r >> e[i].w;
	}
	sort( e+1, e+n+1 , cmp);
	memset( f, 0x3f, sizeof(f));
	f[s] = 0;
	int ans = 0x3f3f3f3f;
	for ( int i = 1; i <= n; i++){
		for (int j = e[i].l-1; j < e[i].r; j++){
			f[e[i].r] = min( f[e[i].r], f[j] + e[i].w);
		}
		if ( e[i].l <= t && e[i].r >= t)ans = min(ans, f[e[i].r]);
	}
	if (ans == 0x3f3f3f3f ) cout << -1 ;
	else cout << ans;
	return 0;
}

然后正解有线段树优化DP  单调栈优化DP

但是有一种最短路算法。

直接上代码：

#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int maxn=10005*10*3;
int n;
struct edge{
	int to,next,w;
}e[maxn];int head[maxn],cnt=0;
void add(int x,int y,int z){
	e[++cnt].to=y;e[cnt].next=head[x];e[cnt].w=z;head[x]=cnt;
}
struct node{
	int num;
	long long dis;
	node(){}
	node(int a,ll b){
		num=a;dis=b;
	}
	bool operator < (const node &a)const{
		return a.dis<dis;
	}
};
long long dis[maxn];int vis[maxn];
void Dij(int s){
    memset(dis,0x3f,sizeof(dis));
    std::priority_queue<node> q;
    dis[s]=0;
    q.push(node(s,0));
    while(!q.empty()){
        node t=q.top();int u=t.num;
        if(vis[u]){
            q.pop(); continue;
        }
        q.pop();vis[u]=1;
        for(int i=head[u];i;i=e[i].next){
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].w)  {
                dis[v]=dis[u]+e[i].w;
                q.push(node(v,dis[v]));
            }
        }
    }
}
int main(){
	//freopen("a.in","r",stdin);
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	int s,t;
	cin>>n>>s>>t;
	for(int i=s;i<t;i++){
		add(i+1,i,0);
	}
	for(int i=1;i<=n;i++){
		int x,y,z;cin>>x>>y>>z;
		add(x,y+1,z);
	}
	Dij(s);
	printf("%lld",dis[t+1]==0x3f3f3f3f3f3f3f3f?-1:dis[t+1]);
	return 0;
}