111. Climbing Stairs 【LintCode easy】

Description

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example

Given an example n=3 , 1+1+1=2+1=1+2=3

return 3

又是一道动态规划类的题目，马上做个专题总结一下。先看一下这个题目，爬楼梯问题，爬楼梯的时候，一次跨一个台阶，或者一次跨两个台阶。我们先从最基本的情况来看：

（1）只有一个台阶：那只有一种走法。（2）大于等于2的时候：那就要分情况讨论了，如下图所示：

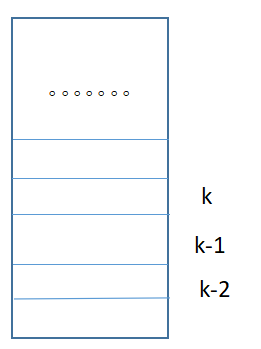
如果想要到达k号台阶，可以选择从k-1号踏上去，也可以选择从k-2号跨过去，但是要先从第0号台阶走到第k-1或者k-2号台阶。走到k-1的方案总数，加上走到k-2的方案总数，就是走到k的方案总数。可以定义一个数组kinds，用kinds[k]来保存走到第k号台阶的方案总数，那么 kinds[k]=kinds[k-1]+kinds[k-2];（其中k>=2）。代码如下：

public class Solution {
    /**
     * @param n: An integer
     * @return: An integer
     */
    public int climbStairs(int n) {
        // write your code here
        if(n==0)
          return 0;
        if(n==1)
          return 1;
        int []kinds=new int[n];
       //初始化第0号和第1号台阶
        kinds[0]=1;
        kinds[1]=2;
        for(int i=2; i<n; i++){
            kinds[i]=kinds[i-1]+kinds[i-2];
        }
      //最后一号便是爬到顶的方案总数
        return kinds[n-1];
    }
}

其实一开始也想到用递归的方法，不过由于递归的次数太多，报了StackOverFlow栈溢出的错误，源代码如下：

public class Solution {
    /**
     * @param n: An integer
     * @return: An integer
     */
    public int climbStairs(int n) {
        // write your code here
        if(n==0)
          return 0;
        if(n==1)
          return 1;
        if(n==2)
          return 2;
        return climbStairs(n-1)+climbStairs(n-2);
    }
}