LightOJ 1214 Large Division

Large Division

　　Given two integers, a and b, you should check whether a is divisible by b or not. We know that an integer a is divisible by an integer b if and only if there exists an integer c such that a = b * c.

Input

　　Input starts with an integer T (≤ 525), denoting the number of test cases.

　　Each case starts with a line containing two integers a (-10²⁰⁰ ≤ a ≤ 10²⁰⁰) and b (|b| > 0, b fits into a 32 bit signed integer). Numbers will not contain leading zeroes.

Output

　　For each case, print the case number first. Then print 'divisible' if a is divisible by b. Otherwise print 'not divisible'.

Sample Input

6

101 101

0 67

-101 101

7678123668327637674887634 101

11010000000000000000 256

-202202202202000202202202 -101

Sample Output

Case 1: divisible

Case 2: divisible

Case 3: divisible

Case 4: not divisible

Case 5: divisible

Case 6: divisible

解题思路：
　　本题考查大数运算，每次测试给定一个整数T为测试数量，之后跟随T行，每行都给出两个数字，第一个数字是一个大于10²⁰⁰  且小于10²⁰⁰的数字，第二个数字是一个32位的int，要求计算第一个数是否可以整除第二个数，若可以整除输出divisible否则输出not divisible。

　　由于第一个数字超出可以直接存储的范围太多，我们不能直接对其进行运算，那么就换一种运算方式，按位对其进行运算，至于如何按位运算，小学时学过对数字运算极为方便的方法——竖式。

　　以12345678 / 9为例子

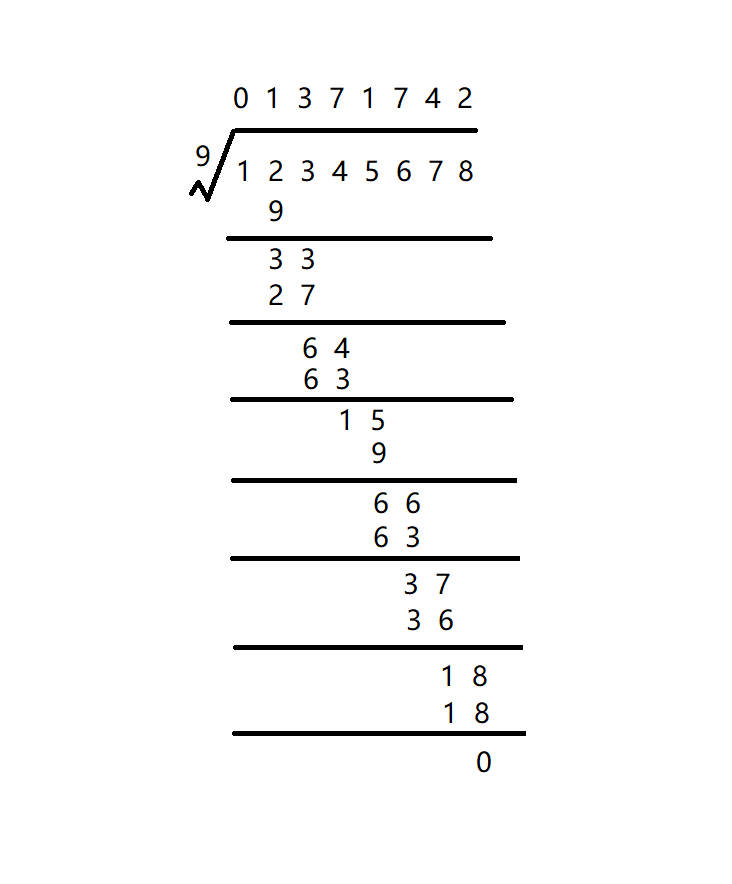
　　由于题目中已经告诉我们输入的数字中不包含先导0，所以按照小学的算法我们用第一个数首位除数除以第二个数，9 除以 1得0余1，继续运算将余数1与下一个数结合得到12， 12除以9得1余3，将3与下一个数结合，得到33，以此类推直到运算到最后一位，我们便可以得到最终的余数。之后判断余数是否为0就可以得出答案。

　　

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int maxn = +;
 struct Big{ //Big储存输入的大数
     int num[maxn];
     int len;
     Big(){
         len = ;
         memset(num, , sizeof(num));
     }
 };
 int divide(Big a, int b){   //传入被除数与除数
     Big c;
     LL mod = ; //mod记路余数
     for(int i = ; i < a.len; i++){ //从首位开始按位运算
         mod = mod *  + a.num[i];  //mod要用long long 因为mod * 10后可能超int范围
         if(mod >= b)    //如果除不开就去计算下一位，除的开就进行计算
             mod = mod % b;  //当前值除以b找到新的余数
     }
    return (int)mod;
 }
 int main()
 {
     int t, b;   //t为测试数量
     string str; //str记录输入第一个数字
     while(scanf("%d", &t) != EOF){
         for(int i = ; i <= t; i++){
             cin >> str >> b;
             Big a;  //a记录第一个数
             if(str[] == '-'){  //第一个数字如果是负数就去掉符号
                 int cnt = ;
                 a.len = str.size() - ;
                 for(string::iterator it = ++str.begin(); it != str.end(); it++){
                     a.num[cnt++] = *it - '';
                 }
             }else{  //正数直接记录入a
                 int cnt = ;
                 a.len = str.size();
                 for(string::iterator it = str.begin(); it != str.end(); it++){
                     a.num[cnt++] = *it - '';
                 }
             }
             if(b < )
                 b = -b;
             if(!divide(a, b)){  //只要mod为0就可以整除，否则不能整除
                 printf("Case %d: divisible\n", i);
             }else{
                 printf("Case %d: not divisible\n", i);
             }
         }
     }
     return ;
 }