Hardmard 变换

阿达马（Hadamard)矩阵是由+1和-1元素构成的正交方阵。阿达马变换多被用来计算SATD(一种视频残差信号大小的衡量)。

这里介绍三个内容，1. SATD 2. H264中阿达马的应用 3. 阿达马变换的构建

1. SATD

SATD是一种视频残差信号大小的衡量标准。

SATD即将残差经哈德曼变换的4×4块的预测残差绝对值总和，可以将其看作简单的时频变换，其值在一定程度上可以反映生成码流的大小。

SATD（Sum of Absolute Transformed Difference）即hadamard变换后再绝对值求和。

2. 在H264中使用4阶和8阶的阿达马变换来计算SATD，变换矩阵为：

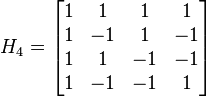
当计算4x4块的SATD时，先使用下面的方法进行二维的阿达马变换：

然后计算所有系数绝对值之和并归一化。

类似的，当计算8x8块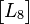的SATD时，先使用下面的方法进行二维的Hadamard变换：

然后计算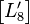所有系数绝对值之和并归一化。

3. 阿达马变换的构建

阿达马变换转换主要型式为 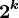 点的转换矩阵，其最小单位矩阵为 2x2 的阿达马变换矩阵，以下分别为二点、四点与如何产生  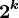点的阿达马变换转换步骤。

• 二点阿达马变换转换：

• 产生 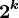 点阿达马变换的步骤：

步骤一： 

步骤二： 根据正负号次序 (Sign change,正负号改变次数) 将矩阵 (Matrix) 内的列向量座顺序上的重新排列。

Hadmard 的 4x4变换，不难理解

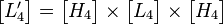
 void hadamard4x4(int **block, int **tblock)
 {
   int i;
   int tmp[];
   int *pTmp = tmp, *pblock;
   int p0,p1,p2,p3;
   int t0,t1,t2,t3;

   // Horizontal
   for (i = ; i < BLOCK_SIZE; i++)
   {
     pblock = block[i];
     p0 = *(pblock++);
     p1 = *(pblock++);
     p2 = *(pblock++);
     p3 = *(pblock  );

     t0 = p0 + p3;
     t1 = p1 + p2;
     t2 = p1 - p2;
     t3 = p0 - p3;

     *(pTmp++) = t0 + t1;
     *(pTmp++) = t3 + t2;
     *(pTmp++) = t0 - t1;
     *(pTmp++) = t3 - t2;
   }

   // Vertical
   for (i = ; i < BLOCK_SIZE; i++)
   {
     pTmp = tmp + i;
     p0 = *pTmp;
     p1 = *(pTmp += BLOCK_SIZE);
     p2 = *(pTmp += BLOCK_SIZE);
     p3 = *(pTmp += BLOCK_SIZE);

     t0 = p0 + p3;
     t1 = p1 + p2;
     t2 = p1 - p2;
     t3 = p0 - p3;

     tblock[][i] = (t0 + t1) >> ;
     tblock[][i] = (t2 + t3) >> ;
     tblock[][i] = (t0 - t1) >> ;
     tblock[][i] = (t3 - t2) >> ;
   }
 }

 void ihadamard4x4(int **tblock, int **block)
 {
   int i;
   int tmp[];
   int *pTmp = tmp, *pblock;
   int p0,p1,p2,p3;
   int t0,t1,t2,t3;

   // Horizontal
   for (i = ; i < BLOCK_SIZE; i++)
   {
     pblock = tblock[i];
     t0 = *(pblock++);
     t1 = *(pblock++);
     t2 = *(pblock++);
     t3 = *(pblock  );

     p0 = t0 + t2;
     p1 = t0 - t2;
     p2 = t1 - t3;
     p3 = t1 + t3;

     *(pTmp++) = p0 + p3;
     *(pTmp++) = p1 + p2;
     *(pTmp++) = p1 - p2;
     *(pTmp++) = p0 - p3;
   }

   //  Vertical
   for (i = ; i < BLOCK_SIZE; i++)
   {
     pTmp = tmp + i;
     t0 = *pTmp;
     t1 = *(pTmp += BLOCK_SIZE);
     t2 = *(pTmp += BLOCK_SIZE);
     t3 = *(pTmp += BLOCK_SIZE);

     p0 = t0 + t2;
     p1 = t0 - t2;
     p2 = t1 - t3;
     p3 = t1 + t3;

     block[][i] = p0 + p3;
     block[][i] = p1 + p2;
     block[][i] = p1 - p2;
     block[][i] = p0 - p3;
   }
 }

Hadmard 变换和反变换（JM18.6)

在JM18.6当中有用到4x2的Hadmard变换。