[matlab] 18.图与网络 (转载)

基本概念：

图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

图论是一种表示 "多对多" 的关系

图是由顶点和边组成的：(可以无边，但至少包含一个顶点)

一组顶点：通常用 V(vertex) 表示顶点集合
一组边：通常用 E(edge) 表示边的集合

图可以分为有向图和无向图，在图中：

(v, w) 表示无向边，即 v 和 w 是互通的
<v, w> 表示有向边，该边始于 v，终于 w

图可以分为有权图和无权图：

有权图：每条边具有一定的权重(weight)，通常是一个数字
无权图：每条边均没有权重，也可以理解为权为 1

图又可以分为连通图和非连通图：

连通图：所有的点都有路径相连
非连通图：存在某两个点没有路径相连

图中的顶点有度的概念：

度(Degree)：所有与它连接点的个数之和
入度(Indegree)：存在于有向图中，所有接入该点的边数之和
出度(Outdegree)：存在于有向图中，所有接出该点的边数之和

图的表示：

图在程序中的表示一般有两种方式：

1. 邻接矩阵：

在 n 个顶点的图需要有一个 n × n 大小的矩阵
在一个无权图中，矩阵坐标中每个位置值为 1 代表两个点是相连的，0 表示两点是不相连的
在一个有权图中，矩阵坐标中每个位置值代表该两点之间的权重，0 表示该两点不相连
在无向图中，邻接矩阵关于对角线相等

2. 邻接链表：

对于每个点，存储着一个链表，用来指向所有与该点直接相连的点
对于有权图来说，链表中元素值对应着权重

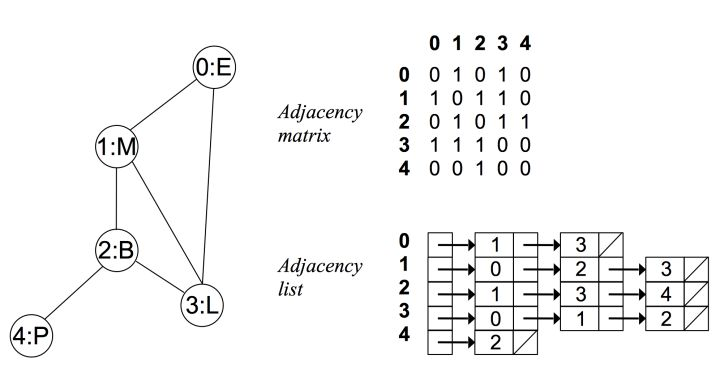
例如在无向无权图中：

在无向有权图中

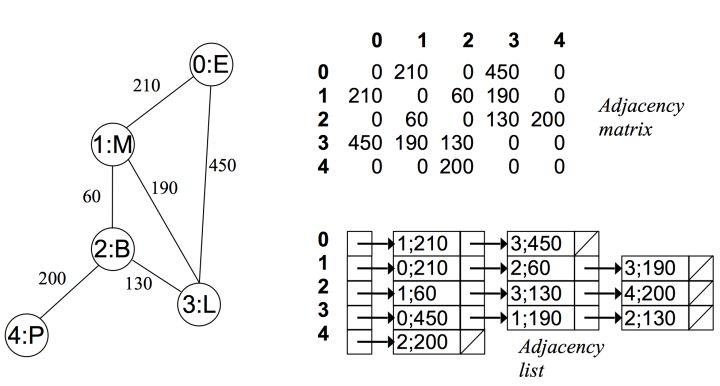
可以看出在无向图中，邻接矩阵关于对角线对称，而邻接链表总有两条对称的边

而在有向无权图中：

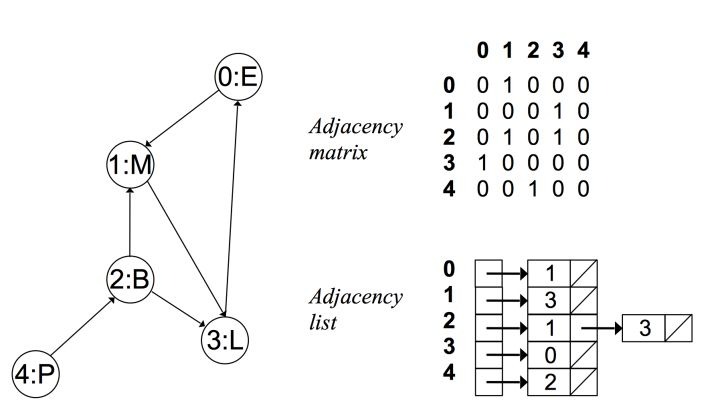
邻接矩阵和链表对比：

邻接矩阵由于没有相连的边也占有空间，因此存在浪费空间的问题，而邻接链表则比较合理地利用空间
邻接链表比较耗时，牺牲很大的时间来查找，因此比较耗时，而邻接矩阵法相比邻接链表法来说，时间复杂度低。

最短路径算法 (Shortest Path Algorithm)

1. 无权图：

问题：在图中找到某一个顶点到其它所有点的距离

对于初始点 v 来说，某个点的 d 代表该点到初始点的距离。

基本步骤：

将所有点的距离 d 设为无穷大
挑选初始点 s，将 ds 设为 0，将 shortest 设为 0
找到所有距离为 d 为 shortest 的点，查找他们的邻接链表的下一个顶点 w，如果 dw 的值为无穷大，则将 dw 设为 shortest + 1
增加 shortest 的值，重复步骤 3，直到没有顶点的距离值为无穷大

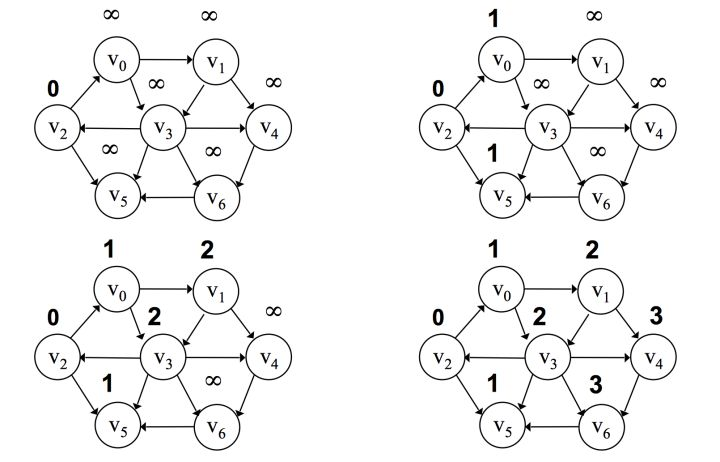
2. 有权图：

在有权图中，常见的最短路径算法有 Dijkstra 算法 Floyd 算法

迪杰斯特拉 Dijkstra 算法：Dijkstra 算法适用于权值为正的的图

Dijkstra 算法属于单源算法，即只能求出某点到其它点最短距离，并不能得出任意两点之间的最短距离。

算法步骤：

将所有边初始化为无穷大
选择一个开始的顶点，添加到优先队列中
对于该点的所有邻接顶点进行判断，如果到该点的距离小于原先的值，则将该值进行更新
将该点所有邻接顶点添加到优先队列中
从优先队列中挑选出一个路径值最小的顶点，将其弹出，作为新的顶点，重复步骤 3，4，5
直到所有点都被处理过一次

例如：

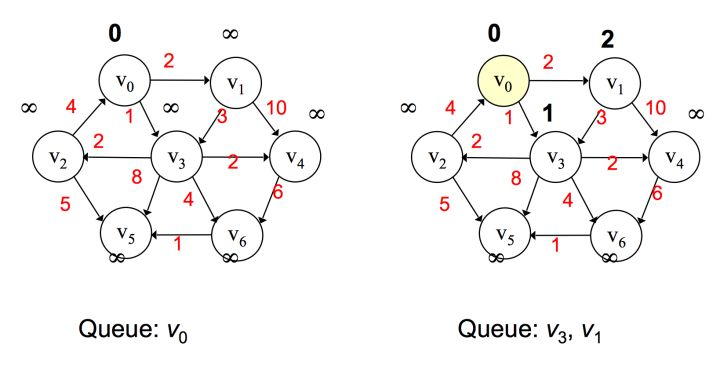
首先选取 v0 作为起始点，添加到优先队列中，将v0弹出，然后对 v0 邻接点进行判断，由于一开始所有边都为无穷大，那么 <v0, v1> 和 <v0, v3> 都更新，值为 2 和 1，按路径大小升序将v3、v1添加到优先队列。

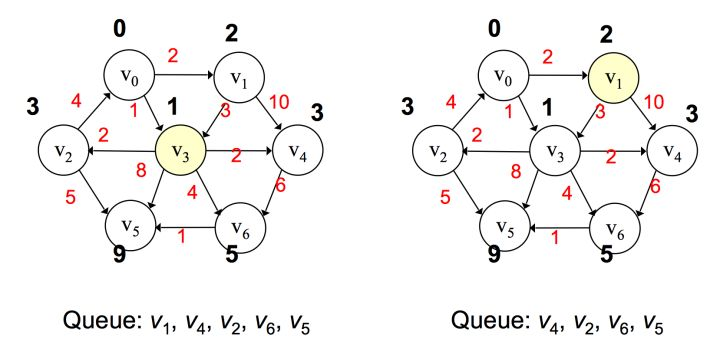
之后将 v3 弹出，对所有 v3 邻接点进行值的更新，并将所有邻接点按路径大小升序添加到优先队列中，若遇到值相同，则无所谓其先后顺序

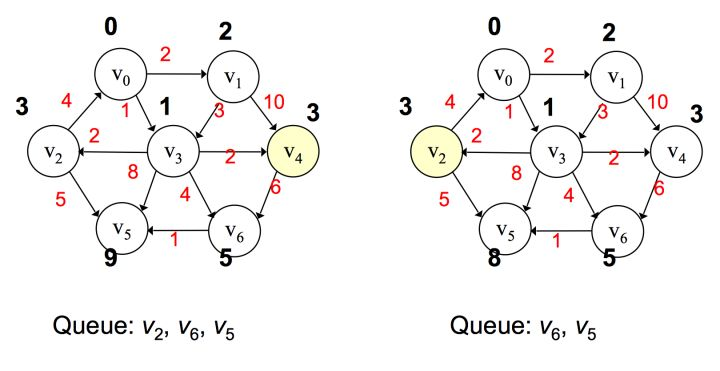
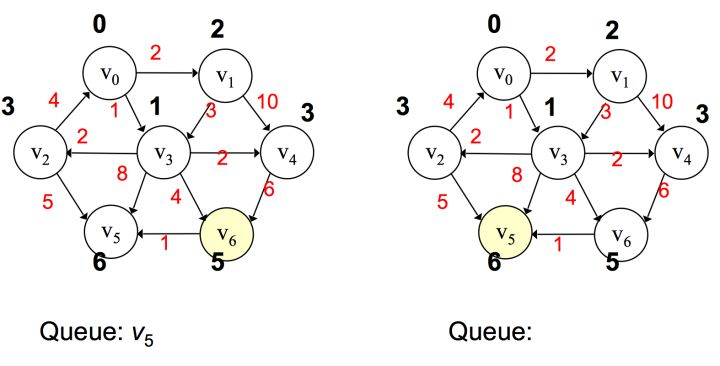
重复这样的过程，直到所有的点都被处理过，则算法终止，这样最后可以得出从 v0 到其它 v1~v6 节点的距离。

Dijkstra 算法适合于权值为正的情况下，若权值为负则不能使用，因为出现死循环。这时候我们需要计算每个顶点被处理的次数，当某个顶点已经处理过的话，就跳出该循环。

佛洛伊德 Floyd 算法：可以求出任意两点的最短距离

Floyd 算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点 i 到点 j 的最短路径。

从任意节点 i 到任意节点 j 的最短路径不外乎 2 种可能：

是直接从 i 到 j
是从 i 经过若干个节点 k 到 j

所以，我们假设 Dis(i,j) 为节点 u 到节点 v 的最短路径的距离，对于每一个节点 k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j) 是否成立，如果成立，证明从 i 到 k 再到 j 的路径比 i 直接到 j 的路径短，我们便设置 Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点 k，Dis(i,j) 中记录的便是 i 到 j 的最短路径的距离。

Dis(i,k) + Dis(k,j) < Dis(i,j),这里的Dis(i,j)来自上一次Dis(i,j)= Dis(i,k) + Dis(k,j),满足了前面式子的小于号之后重新赋值,实现不断更小,最终遍历全图,找到最小值

不断迭代重新赋值

for(int k=0; k<n; k++) {

    for(i=0; i<n; i++) {

         for(j=0; j<n; j++)

             if(A[i][j]>(A[i][k]+A[k][j])) {

                  A[i][j]=A[i][k]+A[k][j];

                  path[i][j]=k;

             }

    }

}

最小生成树 (Minimum Spanning Trees MST)

例如：要在 n 个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

特点：

该树是连通的
权值之和最小
边数比顶点个数少 1

存在个数：最小生成树在一些情况下可能会有多个

当图的每一条边的权值都相同时，该图的所有生成树都是最小生成树
如果图的每一条边的权值都互不相同，那么最小生成树将只有一个

比如：

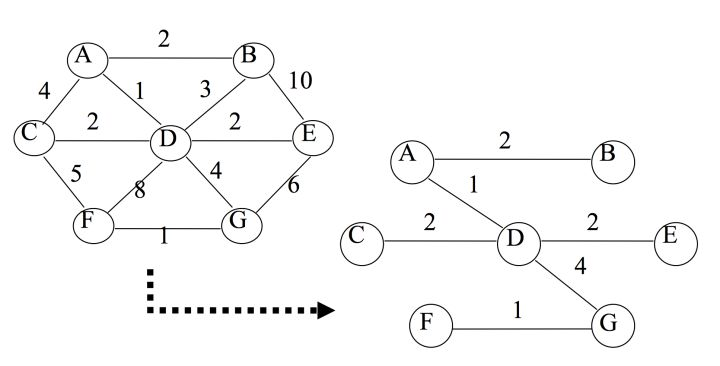
生成最小生成树的算法一般有两种，分别是 Prim 算法和 Kruskal 算法

1. 普里姆算法 (Prim 算法):

算法步骤：

输入：一个加权连通图，其中顶点集合为 V，边集合为 E
初始化：Vnew = {x}，其中 x 为集合 V 中的任一节点(起始点)，Enew = {} 为空
在集合 E 中选取权值最小的边 <u, v>，其中 u 为集合 Vnew 中的元素，而 v 不在 Vnew 集合当中，并且 v∈V (如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）
将 v 加入集合 Vnew 中，将 <u, v> 边加入集合 Enew 中
重复步骤 3、4 直到 Vnew = V

更详细的解释参考维基百科

时间复杂度：O(V^2)

2. Kruskal 算法：需要一个集合用来升序存储所有边

算法步骤：

先构造一个只含有 n 个顶点，而边集为空的子图
从边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图。(也就是说，将这两个顶点分别所在的两棵树合成一棵树) 反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之
重复步骤 2，直到所有点连通

时间复杂度：O( ElogV )

例如：

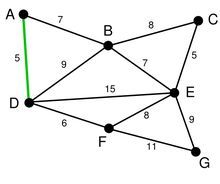
在对所有边进行排序之后，我们得到一个边集合，从边集合中取出最小权的边 AD

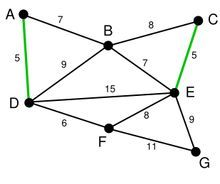
剩下的边中寻找。我们找到了 CE。这里边的权重也是 5，依次类推我们找到了 6,7,7

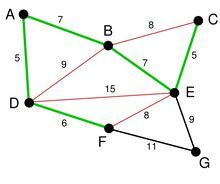
尽管现在长度为 8 的边是最小的未选择的边。但是他们已经连通了

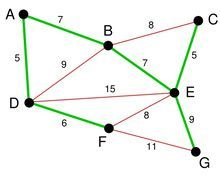
最后就剩下 EG 和 FG 了。当然我们选择了 EG

转载自数据结构与算法系列目录

prim算法

prim是在当前的最小生成树基础上，选择一条最短边作为新的最小生成树。将新加入的点看做一个最小生成树即可。用堆来加速的话，时间复杂度是O(mlogn)O(mlogn)。缺点是空间占用大（因为堆）。由于prim算法需要知道当前点周围的边是什么，一般配合邻接表。

kruskal算法

kruskal算法和prim在思路上的唯一区别就是kruskal每次合并的是一整棵树，而不是一个点。如果用并查集，时间复杂度是O(mlogm)O(mlogm)，优点是代码简单，不过基本上跑不过prim。如果是稠密图时间相差两倍左右，稀疏图则能差到五倍以上。kruskal并不需要每个点周围的边，并且用邻接表做反而麻烦，所以一般选用前向星。