C. A Mist of Florescence ----- Codeforces Round #487 (Div. 2)

C. A Mist of Florescence

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As the boat drifts down the river, a wood full of blossoms shows up on the riverfront.

"I've been here once," Mino exclaims with delight, "it's breathtakingly amazing."

"What is it like?"

"Look, Kanno, you've got your paintbrush, and I've got my words. Have a try, shall we?"

There are four kinds of flowers in the wood, Amaranths, Begonias, Centaureas and Dianthuses.

The wood can be represented by a rectangular grid of nn rows and mm columns. In each cell of the grid, there is exactly one type of flowers.

According to Mino, the numbers of connected components formed by each kind of flowers are aa, bb, cc and dd respectively. Two cells are considered in the same connected component if and only if a path exists between them that moves between cells sharing common edges and passes only through cells containing the same flowers.

You are to help Kanno depict such a grid of flowers, with nn and mm arbitrarily chosen under the constraints given below. It can be shown that at least one solution exists under the constraints of this problem.

Note that you can choose arbitrary nn and mm under the constraints below, they are not given in the input.

Input

The first and only line of input contains four space-separated integers aa, bb, cc and dd (1≤a,b,c,d≤1001≤a,b,c,d≤100) — the required number of connected components of Amaranths, Begonias, Centaureas and Dianthuses, respectively.

Output

In the first line, output two space-separated integers nn and mm (1≤n,m≤501≤n,m≤50) — the number of rows and the number of columns in the grid respectively.

Then output nn lines each consisting of mm consecutive English letters, representing one row of the grid. Each letter should be among 'A', 'B', 'C' and 'D', representing Amaranths, Begonias, Centaureas and Dianthuses, respectively.

In case there are multiple solutions, print any. You can output each letter in either case (upper or lower).

Examples

Input

Copy

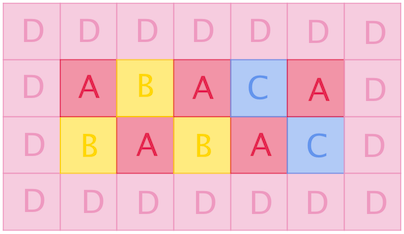
5 3 2 1

Output

Copy

4 7
DDDDDDD
DABACAD
DBABACD
DDDDDDD

Input

Copy

50 50 1 1

Output

Copy

4 50
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
ABABABABABABABABABABABABABABABABABABABABABABABABAB
BABABABABABABABABABABABABABABABABABABABABABABABABA
DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD

Input

Copy

1 6 4 5

Output

Copy

7 7
DDDDDDD
DDDBDBD
DDCDCDD
DBDADBD
DDCDCDD
DBDBDDD
DDDDDDD

Note

In the first example, each cell of Amaranths, Begonias and Centaureas forms a connected component, while all the Dianthuses form one.

嗯 就是一开始把50*50染成四种颜色，然后分别往里面塞不同颜色的块，这样就可以保证，在原有的块是1的情况下，一个一个的加，

当然要注意 每次行要+=2，列也要+=2，防止他们联通成一个，最后需要注意最后一列填充的时候，不要和他旁边的块联通；

一种方法是把D 填充到 A 的区域 这样对着填充，另外也可以不要从第一列开始往后+，从第二列，这样第25列就不会填充了（即每行最多12个）。

每种颜色最多有100个。  
所以每个块最多可以放数量12*12的其他颜色而不影响它自己的连通性。

 #include<iostream>
 #include<cstdio>
 #define For(i,a,b,num) for(int i=a; i<b&&num>0; i+=2)
 using namespace std;
 
 char maps[][];
 
 void paint(int sx,int sy,char word)
 {
     for(int i=sx; i<sx+; ++i){
         for(int j=sy; j<sy+; ++j){
             maps[i][j] = word;
         }
     }
 }
 
 int main()
 {
     int a,b,c,d;
     scanf("%d%d%d%d",&a,&b,&c,&d);
     paint(,,'A');
     paint(,,'B');
     paint(,,'C');
     paint(,,'D');
     a--,b--,c--,d--;
     For(i,,,d){
         For(j,,,d){
             maps[i][j] = 'D';
             d--;
         }
     }
         For(i,,,c){
         For(j,,,c){
             maps[i][j] = 'C';
             c--;
         }
     }
         For(i,,,b){
         For(j,,,b){
             maps[i][j] = 'B';
             b--;
         }
     }
         For(i,,,a){
         For(j,,,a){
             maps[i][j] = 'A';
             a--;
         }
     }
     printf("50 50\n");
     for(int i=; i<; ++i){
         for(int j=; j<; ++j){
             printf("%c",*(maps[i]+j));
         }
         puts("");
     }
 }