本节课内容：

  • 因子分析

---因子分析中的EM步骤的推导过程

  • 主成份分析：有效地降低维度的方法

因子分析

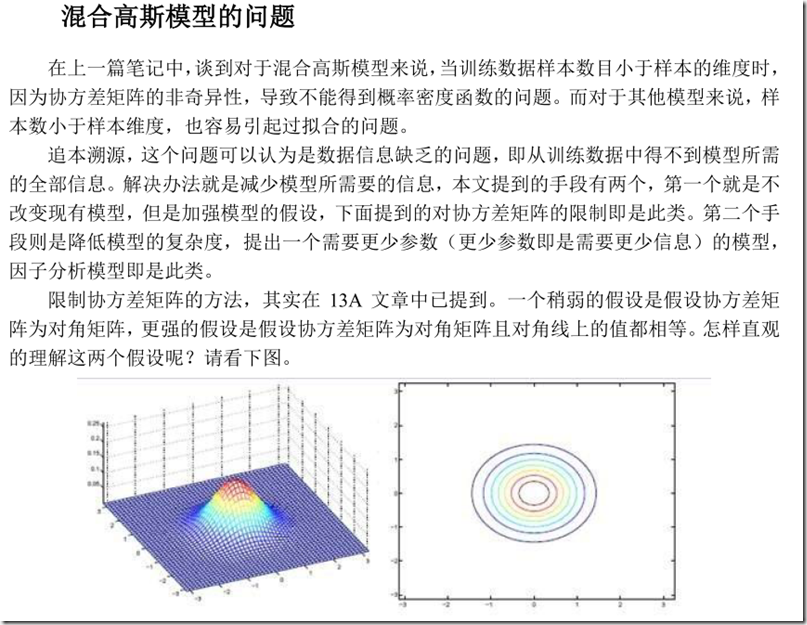
混合高斯模型的问题

接下来讨论因子分析模型，在介绍因子分析模型之前，先看高斯分布的另一种写法，该
写法是推导因子分析模型的基础。

高斯分布的矩阵写法

因子分析模型

因子分析模型的推导

EM 求解参数

PCA(Principal  Components  Analysis,  主成分分析)，也是一种降维方法

主要介绍 PCA(Principal  Components  Analysis,  主成分分析)，也是一种降维方法，但是该方法比较直接，只需计算特征向量就可以进行降维了。

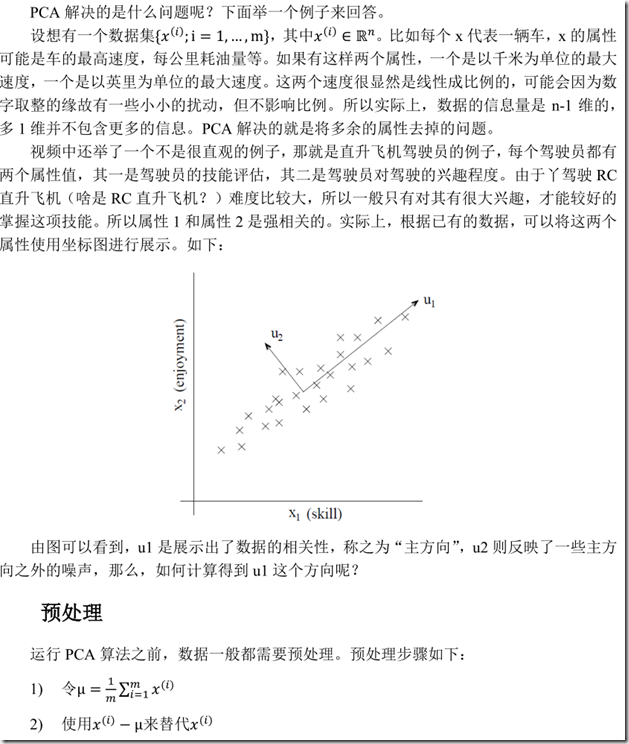
引入

PCA 模型的定义

【cs229-Lecture14】主成分分析法的更多相关文章

  1. 用PCA(主成分分析法)进行信号滤波

    用PCA(主成分分析法)进行信号滤波 此文章从我之前的C博客上导入,代码什么的可以参考matlab官方帮助文档 现在网上大多是通过PCA对数据进行降维,其实PCA还有一个用处就是可以进行信号滤波.网上 ...

  2. 【机器学习】主成分分析法 PCA （II）

    主成分分析法(PAC)的优化——选择主成分的数量 根据上一讲,我们知道协方差为① 而训练集的方差为②. 我们希望在方差尽可能小的情况下选择尽可能小的K值. 也就是说我们需要找到k值使得①/②的值尽可能 ...

  3. 降维之主成分分析法（PCA）

    一.主成分分析法的思想 我们在研究某些问题时,需要处理带有很多变量的数据,比如研究房价的影响因素,需要考虑的变量有物价水平.土地价格.利率.就业率.城市化率等.变量和数据很多,但是可能存在噪音和冗余, ...

  4. （数据科学学习手札22）主成分分析法在Python与R中的基本功能实现

    上一篇中我们详细介绍推导了主成分分析法的原理,并基于Python通过自编函数实现了挑选主成分的过程,而在Python与R中都有比较成熟的主成分分析函数,本篇我们就对这些方法进行介绍: R 在R的基础函 ...

  5. 【转载】主成分分析法（PCA）

    https://www.jisilu.cn/question/252942 进行维数约减(Dimensionality Reduction),目前最常用的算法是主成分分析法 (Principal Co ...

  6. 吴恩达机器学习笔记（八） —— 降维与主成分分析法(PCA)

    主要内容: 一.降维与PCA 二.PCA算法过程 三.PCA之恢复 四.如何选取维数K 五.PCA的作用与适用场合 一.降维与PCA 1.所谓降维,就是将数据由原来的n个特征(feature)缩减为k ...

  7. 机器学习回顾篇（14）：主成分分析法（PCA）

    .caret, .dropup > .btn > .caret { border-top-color: #000 !important; } .label { border: 1px so ...

  8. 主成分分析法（PCA）原理和步骤

    主成分分析法(PCA)原理和步骤 主成分分析(Principal Component Analysis,PCA)是一种多变量统计方法,它是最常用的降维方法之一,通过正交变换将一组可能存在相关性的变量数 ...

  9. 【笔记】主成分分析法PCA的原理及计算

    主成分分析法PCA的原理及计算 主成分分析法 主成分分析法(Principal Component Analysis),简称PCA,其是一种统计方法,是数据降维,简化数据集的一种常用的方法 它本身是一 ...

  10. 特征脸(Eigenface)理论基础-PCA(主成分分析法)

    在之前的博客  人脸识别经典算法一:特征脸方法(Eigenface)  里面介绍了特征脸方法的原理,但是并没有对它用到的理论基础PCA做介绍,现在做补充.请将这两篇博文结合起来阅读.以下内容大部分参考 ...

随机推荐

  1. numpy中dtype

    简单说明dtype使用方法: Rule为规则类,其中有3个字段,1为类型,2为计算规则,3为保留位数 如 :'close': Rule(float64, 1 / 10000.0, 2), 表示收盘价, ...

  2. js 操作json对象增删改

    //将表单序列化成字符串 $.fn.serializeObject = function () { var obj = {}; var count = 0; $.each(this.serialize ...

  3. 每天一个linux命令：pwd命令

    Linux中用 pwd 命令来查看”当前工作目录“的完整路径. 简单得说,每当你在终端进行操作时,你都会有一个当前工作目录. 在不太确定当前位置时,就会使用pwd来判定当前目录在文件系统内的确切位置. ...

  4. C# 反射(GetType) 获取动态Json对象属性值的方法

    之前在开发一个程序,希望能够通过属性名称读取出属性值,但是由于那时候不熟悉反射,所以并没有找到合适的方法,做了不少的重复性工作啊! 然后今天我再上网找了找,被我找到了,跟大家分享一下. 其实原理并不复 ...

  5. 【玩转Golang】 自定义json序列化对象时，非法字符错误原因

    由于前台web页面传来的日期对象是这样的格式“2010-11-03 15:23:22”,所以我安装网上查来的办法,自定义包装了time.Time对象,实现自己的Marshal和UnMarshal方法 ...

  6. mocha框架下，异步测试代码错误造成的问题----用例超时错误

    今天用抹茶(mocha)做个测试,发现有一个测试项目总是超时: describe("DbFactory functions",function(){ it("query ...

  7. iOS多版本多设备适配的问题

    好吧,能找到这文章的,一般是接到了如下需求:  我是从raywenderlich抽了点内容出来做日记,另外,本文说的不是布局的适配,而是因为ios的升级带来的各版本代码上的不兼容. Deploymen ...

  8. 【VirtualBox】ubuntu虚拟机与windows设置共享文件夹

    第一步:配置 http://blog.csdn.net/a962804835/article/details/72820355 第二步:解决ubuntu下共享文件夹无访问权限的问题 http://bl ...

  9. DOS 配置IP地址

    @echo off :startIP set /p source=STATIC Y or N or E: echo source:%source% if "%source%" == ...

  10. NetBpm 示例：请假审批(6)

    转载注明出处: http://www.cnblogs.com/anbylau2130/p/3877983.html 原文: 请假示例 流程定义包源码下载(注:par包就是zip格式压缩包).原文地址: ...