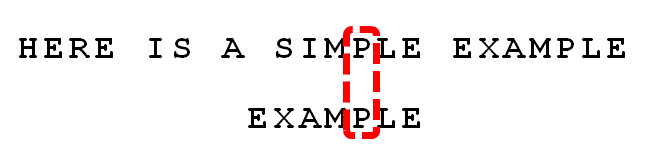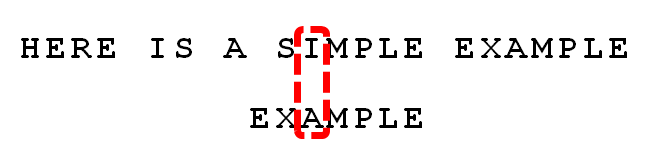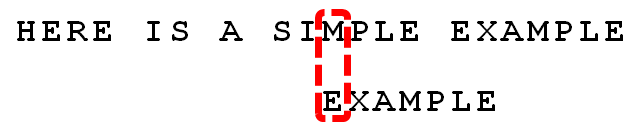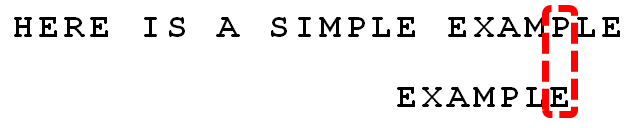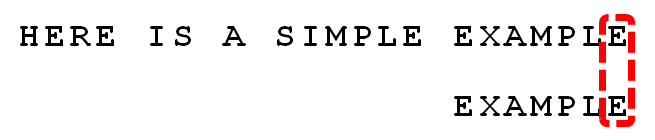字符串匹配 扩展KMP BM&Sunday
复杂度都是O(n)
扩展1:BM算法
KMP的匹配是从模式串的开头开始匹配的,而1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了一种新的字符串匹配算法:Boyer-Moore算法,简称BM算法。该算法从模式串的尾部开始匹配,且拥有在最坏情况下O(N)的时间复杂度。在实践中,比KMP算法的实际效能高。
BM算法定义了两个规则:
- 坏字符规则:当文本串中的某个字符跟模式串的某个字符不匹配时,我们称文本串中的这个失配字符为坏字符,此时模式串需要向右移动,移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外,如果"坏字符"不包含在模式串之中,则最右出现位置为-1。
- 好后缀规则:当字符失配时,后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置,且如果好后缀在模式串中没有再次出现,则为-1。
下面举例说明BM算法。例如,给定文本串“HERE IS A SIMPLE EXAMPLE”,和模式串“EXAMPLE”,现要查找模式串是否在文本串中,如果存在,返回模式串在文本串中的位置。
1. 首先,"文本串"与"模式串"头部对齐,从尾部开始比较。"S"与"E"不匹配。这时,"S"就被称为"坏字符"(bad character),即不匹配的字符,它对应着模式串的第6位。且"S"不包含在模式串"EXAMPLE"之中(相当于最右出现位置是-1),这意味着可以把模式串后移6-(-1)=7位,从而直接移到"S"的后一位。
2. 依然从尾部开始比较,发现"P"与"E"不匹配,所以"P"是"坏字符"。但是,"P"包含在模式串"EXAMPLE"之中。因为“P”这个“坏字符”对应着模式串的第6位(从0开始编号),且在模式串中的最右出现位置为4,所以,将模式串后移6-4=2位,两个"P"对齐。
. 依次比较,得到 “MPLE”匹配,称为"好后缀"(good suffix),即所有尾部匹配的字符串。注意,"MPLE"、"PLE"、"LE"、"E"都是好后缀。
. 发现“I”与“A”不匹配:“I”是坏字符。如果是根据坏字符规则,此时模式串应该后移2-(-1)=3位。问题是,有没有更优的移法?
. 更优的移法是利用好后缀规则:当字符失配时,后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串中上一次出现的位置,且如果好后缀在模式串中没有再次出现,则为-1。
所有的“好后缀”(MPLE、PLE、LE、E)之中,只有“E”在“EXAMPLE”的头部出现,所以后移6-0=6位。
可以看出,“坏字符规则”只能移3位,“好后缀规则”可以移6位。每次后移这两个规则之中的较大值。这两个规则的移动位数,只与模式串有关,与原文本串无关。
6. 继续从尾部开始比较,“P”与“E”不匹配,因此“P”是“坏字符”,根据“坏字符规则”,后移 6 - 4 = 2位。因为是最后一位就失配,尚未获得好后缀。
由上可知,BM算法不仅效率高,而且构思巧妙,容易理解。
扩展2:Sunday算法
- Sunday算法是从前往后匹配,在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。
- 如果该字符没有在模式串中出现则直接跳过,即移动位数 = 匹配串长度 + 1;
- 否则,其移动位数 = 模式串中最右端的该字符到末尾的距离+1。
下面举个例子说明下Sunday算法。假定现在要在文本串"substring searching algorithm"中查找模式串"search"。
1. 刚开始时,把模式串与文本串左边对齐:
substring searching algorithm
search
^
2. 结果发现在第2个字符处发现不匹配,不匹配时关注文本串中参加匹配的最末位字符的下一位字符,即标粗的字符 i,因为模式串search中并不存在i,所以模式串直接跳过一大片,向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7,从 i 之后的那个字符(即字符n)开始下一步的匹配,如下图:
substring searching algorithm
search
^
3. 结果第一个字符就不匹配,再看文本串中参加匹配的最末位字符的下一位字符,是'r',它出现在模式串中的倒数第3位,于是把模式串向右移动3位(r 到模式串末尾的距离 + 1 = 2 + 1 =3),使两个'r'对齐,如下:
substring searching algorithm
search
^
4. 匹配成功。
回顾整个过程,我们只移动了两次模式串就找到了匹配位置,缘于Sunday算法每一步的移动量都比较大,效率很高。完。
字符串匹配 扩展KMP BM&Sunday的更多相关文章
- 字符串匹配--扩展KMP模板
对于一个字符串 s 以及子串 t ,扩展KMP可以用来求 t 与 s 的每个子串的最长公共前缀 ext [ i ],当然,如果有某个 ext 值等于 t 串的长度 lent ,那么就说明从其对应的 i ...
- HDU 1711 Number Sequence (字符串匹配,KMP算法)
HDU 1711 Number Sequence (字符串匹配,KMP算法) Description Given two sequences of numbers : a1, a2, ...... , ...
- Luogu 3375 【模板】KMP字符串匹配(KMP算法)
Luogu 3375 [模板]KMP字符串匹配(KMP算法) Description 如题,给出两个字符串s1和s2,其中s2为s1的子串,求出s2在s1中所有出现的位置. 为了减少骗分的情况,接下来 ...
- 字符串匹配的 KMP算法
一般字符串匹配过程 KMP算法是字符串匹配算法的一种改进版,一般的字符串匹配算法是:从主串(目标字符串)和模式串(待匹配字符串)的第一个字符开始比较,如果相等则继续匹配下一个字符, 如果不相等则从主串 ...
- 字符串匹配的kmp算法 及 python实现
一:背景 给定一个主串(以 S 代替)和模式串(以 P 代替),要求找出 P 在 S 中出现的位置,此即串的模式匹配问题. Knuth-Morris-Pratt 算法(简称 KMP)是解决这一问题的常 ...
- HDU 2087 剪花布条(字符串匹配,KMP)
HDU 2087 剪花布条(字符串匹配,KMP) Description 一块花布条,里面有些图案,另有一块直接可用的小饰条,里面也有一些图案.对于给定的花布条和小饰条,计算一下能从花布条中尽可能剪出 ...
- HDU 1686 Oulipo / POJ 3461 Oulipo / SCU 2652 Oulipo (字符串匹配,KMP)
HDU 1686 Oulipo / POJ 3461 Oulipo / SCU 2652 Oulipo (字符串匹配,KMP) Description The French author George ...
- 字符串匹配(KMP 算法 含代码)
主要是针对字符串的匹配算法进行解说 有关字符串的基本知识 传统的串匹配法 模式匹配的一种改进算法KMP算法 网上一比較易懂的解说 小样例 1计算next 2计算nextval 代码 有关字符串的基本知 ...
- leetcode28 strstr kmp bm sunday
字符串匹配有KMP,BM,SUNDAY算法. 可见(https://leetcode-cn.com/problems/implement-strstr/solution/c5chong-jie-fa- ...
随机推荐
- javascript的闭包计数器实现,python实现各种方法来实现计数器
菜鸟教程的javascript闭包章节中,演示了js计数器的实现. 教程地址 http://www.runoob.com/js/js-function-closures.html 代码1 var ...
- c#中如何退出程序后自动重新启动程序
//触发退出程序事件 private void button1_Click(object sender, EventArgs e) { Application.E ...
- Hibernate的Configuration和SessionFactiory
Configuration: Configuration是hibernate的入口,负责管理Hibernate的配置信息,这些配置信息都是从配置文件hibernate.cfg.xml或者Hiberna ...
- 对象克隆技术Object.clone()
Java中对象的创建 clone顾名思义就是复制, 在Java语言中, clone方法被对象调用,所以会复制对象. 所谓的复制对象,首先要分配一个和源对象同样大小的空间,在这个空间中创建一个新的对象. ...
- 8 -- 深入使用Spring -- 7...1 启动Spring 容器
8.7.1 启动Spring容器 对于使用Spring的Web应用,无须手动创建Spring容器,而是通过配置文件声明式地创建Spring容器.因此,在Web应用中创建Spring容器有如下两种方式: ...
- RabbitMQ :VHost,Exchanges, Queues,Bindings and Channels
和RabbitMQ这个项目的缘分好奇怪,很长一段时间内是只关注源代码,真的是Erlang开源项目中的典范;现在要在项目中应用RabbitMQ,从新的视角切入,全新的感觉.仿佛旧情人换了新衣,虽是熟稔却 ...
- java里面的getAttribute和findAttribute的区别
findAttribute: abstract Object findAttribute(String name) Searches for the named attribute in page, ...
- iOS - UITabBarController中的坑
当你创建一个继承与UITabBarController的子类 并想给其自定义构造方法 传一些值的时候这时候问题出现了: 在创建的时候里面的init方法回调用了 viewdidload,导致每次传值的时 ...
- 微信redirect_uri 回调错误,scope权限错误
scope权限错误以及微信redirect_uri回调错误 昨天修改项目的时候,初始时,因为项目最开始使用的是第三方授权处理,拿到的用户openid是第三方账号的,所以需要将获取对方信息的代码修改.只 ...
- WP8.1学习系列(第二十四章)——Json解析
.net已经集成了json解析,类名叫DataContractJsonSerializer DataContractJsonSerializer 类型公开以下成员. 构造函数 名称 说明 Da ...