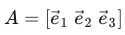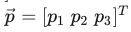PCA(Principal Components Analysis)主成分分析: 坐标基 + 基变换 + 一维列向量坐标的变换: 左乘变换矩阵 而 一维行向量的坐标系基元的变换 是 右乘变换矩阵
https://zhuanlan.zhihu.com/p/661060377
总结:
- 坐标与坐标系(基向量组=变换矩阵)是成对出现。同一点在不同坐标系的坐标的变换,要有统一的“世界坐标系”
- 坐标(一维列向量)变换: 左乘 变换矩阵;只是改变“视角”,都是同一点在不同坐标系去描述
- 基元(一维行向量)变换: 右乘 变换矩阵;基元(坐标系)发生改变, 是将一坐标系转为新坐标系
类比:
- 长度的数值与单位是成对出现,
- 同一物体的长度L,需要有统一的metrics公米制才可以进行换算:
Feet(US), Inch(UK), Miles, nautical(sea) Miles, Yards, Light-Year; - 长度变换:物体的长度始终是 1m, 在不同制的尺测量值有:
1m = 3.2808333Feet(US) = 39.370079Inch(UK)
= 0.00062Miles = 0.00054Naut.Miles = 1.094Yards. - 测度制变换:Inch制测度尺 变换到 Metrics制测度尺。
测度高维空间的点的位置需要:
- 建立坐标系:首先建立坐标系,选择哪些维度,每个维度的参考点;
- 其次将点位置投射到此坐标系的每一维度,得到对应维度上的测度;
- 正式表示:表示坐标系的坐标基矩阵乘上点坐标(该坐标系上的)。
数学表示: 坐标系的坐标基矩阵乘上点坐标(该坐标系上的):
️注意:以下表达式的小写字母:头上有 “\(\large \rightarrow\)”的是\(\large vector\);没有的是\(\large Scalar\);
在描述空间的某个点时可以将其描述为: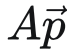
坐标系的坐标基矩阵乘上点坐标(该坐标系上的).
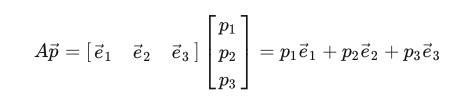
- 此空间坐标系A的坐标基矩阵(本文坐标系的基向量都为标准正交基):
![]()
- 此空间的p点在坐标系A的点坐标:
![]()
也可以将其看成世界坐标系的点坐标(世界坐标系以单位阵为坐标系坐标基矩阵):
引入世界坐标系的必要性: 是因为它将在后续的 坐标变换 及 坐标系变换,充当转换站的Role。
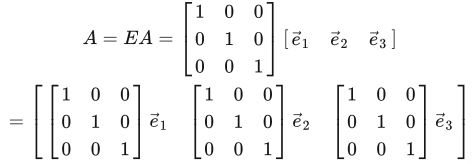
上式的单位阵为:

坐标变换与坐标系变换
实际应用经常会遇到多个坐标系以及其对应的坐标的情况,比如:
坐标系A及其对应的坐标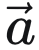 和 坐标系B及其坐标
和 坐标系B及其坐标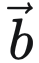 。
。
我们假设它们之间存在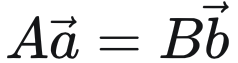 , 也就是空间的同一个点用不同坐标系下的坐标来描述。因此有:
, 也就是空间的同一个点用不同坐标系下的坐标来描述。因此有: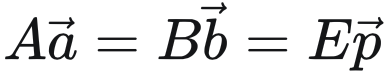
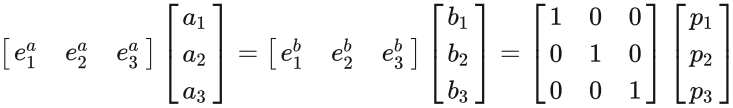
上式的基向量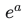 代表它是坐标系A的基向量,同时实际上也等于世界坐标系乘以世界坐标的形式即
代表它是坐标系A的基向量,同时实际上也等于世界坐标系乘以世界坐标的形式即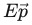 。
。
坐标系A实际上是对世界坐标系进行A对应的初等列变换后得到的。
坐标系A的每个列向量,事实上都是对世界坐标系的三个基向量进行线性加和后得到的。
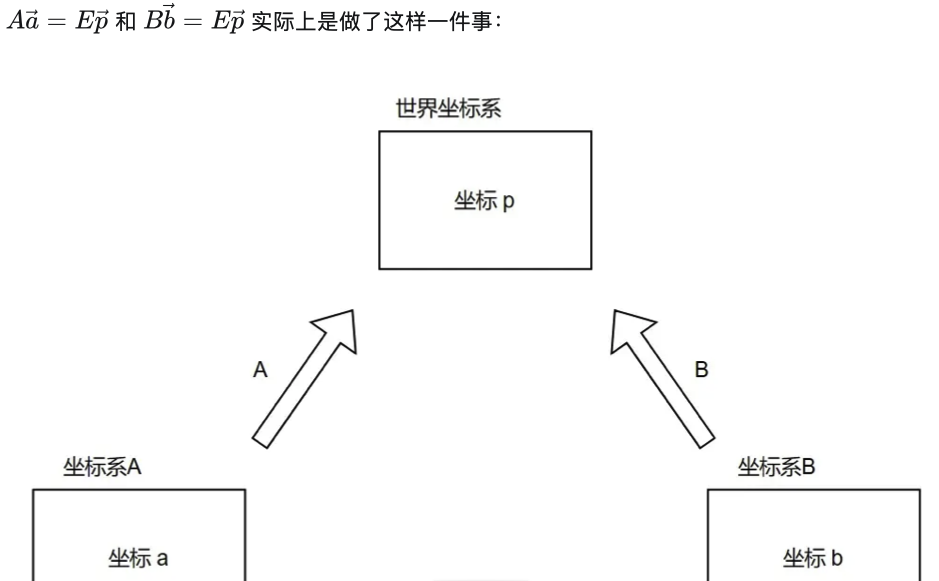
将 坐标系A上的坐标a 与 坐标系B上的坐标b 转化为 世界坐标系上的坐标p :
![]()
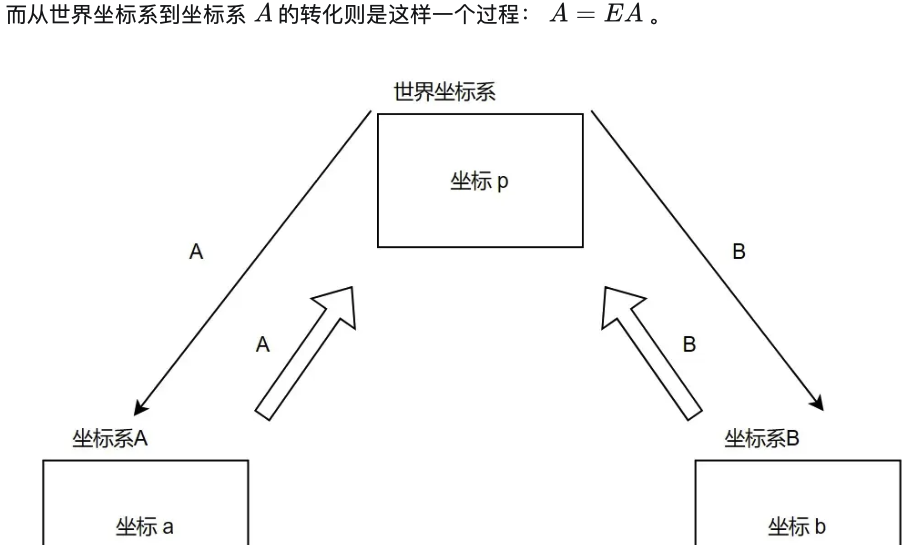
世界坐标系到坐标系A或B的转化过程则是:
![]()
坐标变换
坐标变换定义:把一个向量(或一个点)从一个高维(或3D)坐标系,转换到另一个高维(或3D)坐标系去。
通过将旧坐标A0, 左乘一个变换矩阵 T, 就可以实现。注意:坐标变换 是 左乘(变换矩阵T 是 乘在左边)的。 变换: T * A0 = A1, 此处 旧坐标A0,新坐标A1 都是一维列向量;
坐标变换矩阵 T 乘在左边 是因为坐标多是用一维列向量表示,因此过渡矩阵A只能被乘到左边。
坐标系基元(基元为一维行向量)的变换 是 右乘 变换矩阵,举个栗子就可以分清:
已知坐标系基元为 (i, j, k),基元为一维行向量表示, 因而基元的变换只能是右乘.
举个栗子:A1.shape(1,3)= A0.shape(1, 3) * T.shape(3,3)。
PCA(Principal Components Analysis)主成分分析: 坐标基 + 基变换 + 一维列向量坐标的变换: 左乘变换矩阵 而 一维行向量的坐标系基元的变换 是 右乘变换矩阵的更多相关文章
- PCA(Principal Components Analysis)主成分分析
全是图片..新手伤不起.word弄的,结果csdn传不了..以后改. .
- A tutorial on Principal Components Analysis | 主成分分析(PCA)教程
A tutorial on Principal Components Analysis 原著:Lindsay I Smith, A tutorial on Principal Components A ...
- 主成分分析 | Principal Components Analysis | PCA
理论 仅仅使用基本的线性代数知识,就可以推导出一种简单的机器学习算法,主成分分析(Principal Components Analysis, PCA). 假设有 $m$ 个点的集合:$\left\{ ...
- 主成分分析(principal components analysis, PCA)
原理 计算方法 主要性质 有关统计量 主成分个数的选取 ------------------------------------------------------------------------ ...
- 主成分分析(principal components analysis, PCA)——无监督学习
降维的两种方式: (1)特征选择(feature selection),通过变量选择来缩减维数. (2)特征提取(feature extraction),通过线性或非线性变换(投影)来生成缩减集(复合 ...
- [zz] Principal Components Analysis (PCA) 主成分分析
我理解PCA应该分为2个过程:1.求出降维矩阵:2.利用得到的降维矩阵,对数据/特征做降维. 这里分成了两篇博客,来做总结. http://matlabdatamining.blogspot.com/ ...
- 从矩阵(matrix)角度讨论PCA(Principal Component Analysis 主成分分析)、SVD(Singular Value Decomposition 奇异值分解)相关原理
0. 引言 本文主要的目的在于讨论PAC降维和SVD特征提取原理,围绕这一主题,在文章的开头从涉及的相关矩阵原理切入,逐步深入讨论,希望能够学习这一领域问题的读者朋友有帮助. 这里推荐Mit的Gilb ...
- Jordan Lecture Note-9: Principal Components Analysis (PCA).
Principal Components Analysis (一)引入PCA 当我们对某个系统或指标进行研究时往往会发现,影响这些系统和指标的因素或变量的数量非常的多.多变量无疑会为科学研究带来 ...
- Stat2—主成分分析(Principal components analysis)
最近在猛撸<R in nutshell>这本课,统计部分涉及的第一个分析数据的方法便是PCA!因此,今天打算好好梳理一下,涉及主城分析法的理论以及R实现!come on…gogogo… 首 ...
- Andrew Ng机器学习公开课笔记–Principal Components Analysis (PCA)
网易公开课,第14, 15课 notes,10 之前谈到的factor analysis,用EM算法找到潜在的因子变量,以达到降维的目的 这里介绍的是另外一种降维的方法,Principal Compo ...
随机推荐
- Windows 提权指南
男儿若遂平生志,五经勤向窗前读. 导航 壹 - Se 特权 贰 - RunAs 叁 - 弱服务 肆 - Windows 内核 伍 - 密码搜寻 陆 - 杂项 AlwaysInstallElevated ...
- jetbrains这是作啥妖呢,用了好久都没有问题,现在这是咋了?
rider今天更新了下2025.1 数据库驱动下载不来: 插件不能正常访问: 清理下用户的配置目录: %UserProfile%\AppData\Local\JetBrains %UserProfil ...
- SpringBoot文件上传--转载
转载地址:https://www.jianshu.com/p/85017f5ecba1
- 从零开始学Flink:开启实时计算的魔法之旅
在凌晨三点的数据监控大屏前,某电商平台的技术负责人突然发现一个异常波动:支付成功率骤降15%.传统的数据仓库此时还在沉睡,而基于Flink搭建的实时风控系统早已捕捉到这个信号,自动触发预警机制.当运维 ...
- 行为模式 -- 观察者模式(Observer)
Observer(观察者模式) -- 对象行为型模式 别名 依赖,发布-订阅(publish - subscribe) 意图 定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时,所有依赖于它 ...
- RPC实战与核心原理之流量回放
流量回放:保障业务技术升级的神器 回顾 时钟轮在 RPC 中的应用,核心原理就一个关键字"分而治之",我们可以把它用在任何需要高效处理大量定时任务的场景中,最具有代表性的就是在高并 ...
- codeup之找x
Description 输入一个数n,然后输入n个数值各不相同,再输入一个值x,输出这个值在这个数组中的下标(从0开始,若不在数组中则输出-1). Input 测试数据有多组,输入n(1<=n& ...
- 一个大对象引起的血案,GC的踩坑实录
背景: 问题: 有个渠道支付服务,负责与所有支付相关服务进行交互,包括 渠道下单支付,渠道成功通知,渠道的对账等 服务4台机,平时跑的都很稳定,通过thrift进行对外提供服务,且平时并未发现访问 ...
- 开发AR导航助手:ARKit+Unity+Mapbox全流程实战教程
引言 在增强现实技术飞速发展的今天,AR导航应用正逐步改变人们的出行方式.本文将手把手教你使用Unity+ARKit+Mapbox开发跨平台AR导航助手,实现从虚拟路径叠加到空间感知的完整技术闭环.通 ...
- CF contest 1909 Pinely Round 3 (Div. 1 + Div. 2) 题解(Vanilla的掉分赛)
CF contest 1909 Pinely Round 3 (Div. 1 + Div. 2) Vanilla的掉分赛 绪言 Pinely Round 3 (Div. 1 + Div. 2) - C ...