The 2023 ICPC Asia Hong Kong Regional Programming Contest

A. TreeScript

给你一个根，让你构造一棵树，每个节点被创造的时候必须知道它的父节点的地址和需要寄存器存放当前节点的地址，现在给定你每个节点之间的关系，并且现在根节点已经被创建，且有一个寄存器存放着根节点的地址，请问最少需要几个寄存器才能构造出这颗完整的树

题解：树形\(DP\)

我们先来分析一下样例：

  1. 0 1 2，ans = 1，代表:\(1->2->3\),一开始1号根节点处有一个寄存器，那么创建节点2的时候，我们需要可以不需要多余的寄存器，我们只要将节点2的地址覆盖根节点处寄存器中存放的节点1的地址即可，也就是说节点2继承了节点1的寄存器，对于节点3同理，继承了节点2的寄存器

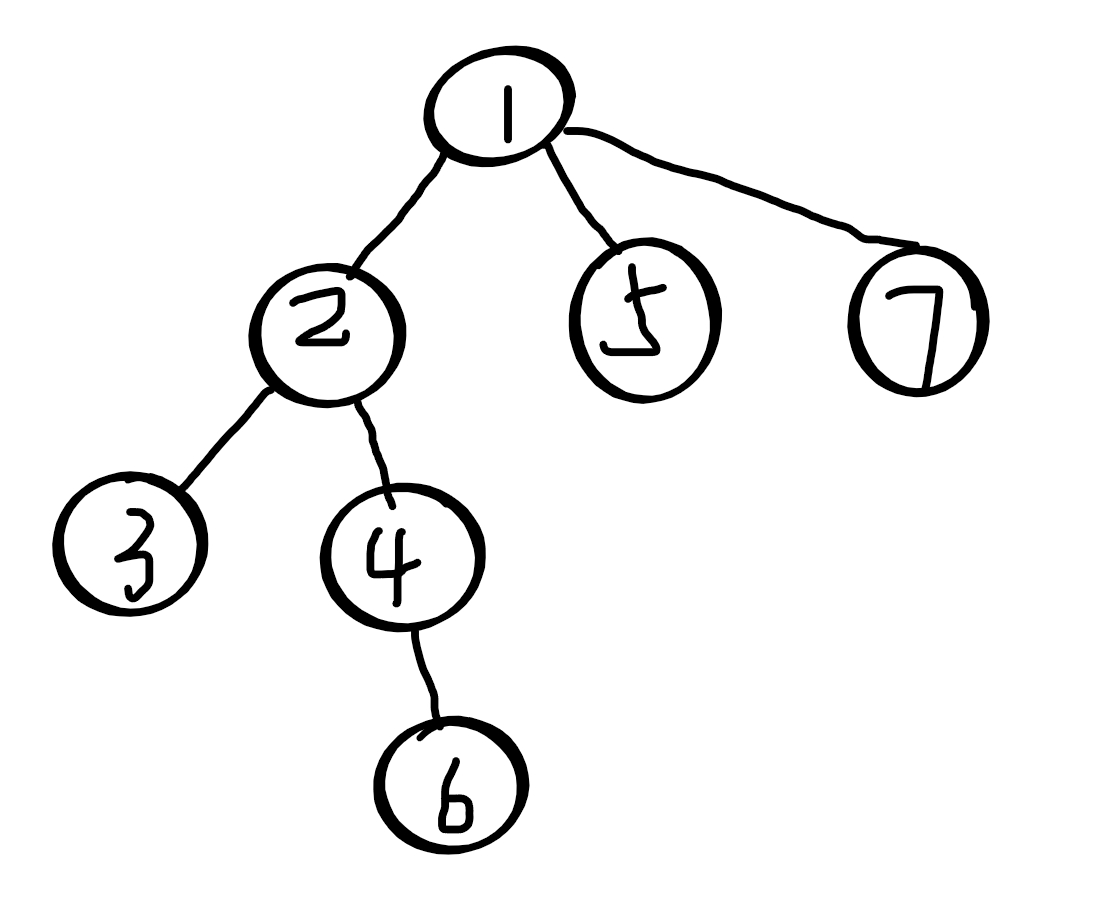
  2. 0 1 2 2 1 4 1，ans = 2

我们贪心的先创建小子树，发现我们在创建节点7的时候我们不能覆盖节点1的地址，也就是说我们不能继承节点1的寄存器，因为创建节点5和节点2的时候我们需要知道节点1的地址，所以我们创建节点7的时候需要新创建1个寄存器来存放节点7的地址；在创建节点5的时候我们可以继承节点7的寄存器，同理节点2也可以继承节点5的寄存器，所以我们发现我们贪心的创建从小子树到大子树的过程，大子树可以继承小子树的寄存器；对于节点2来说它还有子节点没有建立，所以我们需要建立2的子树，这个时候根节点1处的寄存器就没有用处了，可以用于创建节点3，然后创建节点4，再然后继承给节点6，这样一颗树就建完了，所以只用到了两个寄存器

通过模拟上述两个样例我们得知：

  1. 我们贪心从小子树的建立开始，到大子树结束，并且最后一颗最大的子树还能继承根节点的寄存器
  2. 如果根节点的子节点没有建立完，那么根节点处的寄存器不能被继承
  3. 以\(u\)节点为根，它需要的寄存器数量是建立次大子树\(v_2\)需要的寄存器加上根节点上的寄存器（因为最后最大子树会继承两者之和）和建立最大子树\(v_1\)需要的寄存器两者之间取\(max\)

状态表示：\(f[u]\):以\(u\)为根节点的子树被创建所需的寄存器数量

状态属性：数量

状态转移：\(f[u] = max(f[v_1],f[v_2]+1),v_1>=v_2>=v_3..\)

状态初始：\(f[u] = 1\)

#include <bits/stdc++.h>

#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)

#define debug(x) cerr << #x << '=' << x << endl

#define all(x) (x).begin(), (x).end()

#define rson id << 1 | 1

#define lson id << 1

#define int long long

#define mpk make_pair

#define endl '\n'

using namespace std;

typedef unsigned long long ULL;

typedef long long ll;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

const int inf = 0x3f3f3f3f;

const ll INF = 0x3f3f3f3f3f3f3f3f;

const int mod = 1e9 + 7;

const double eps = 1e-9;

const int N = 2e5 + 10, M = 4e5 + 10;

int n;

vector<int> g[N];

int f[N];

void dfs(int u, int par)

{

    f[u] = 1;

    for (auto v : g[u])

    {

        if (v == par)

            continue;

        dfs(v, u);

        f[u] = max(f[u], f[v]);

    }

    int cnt = 0;

    for (auto v : g[u])

    {

        if (v == par)

            continue;

        if (f[u] == f[v])

            cnt++;

    }

    if (cnt > 1)

        f[u]++;

}

void solve()

{

    cin >> n;

    for (int i = 1; i <= n; ++i)

        g[i].clear();

    for (int i = 1, u; i <= n; ++i)

    {

        cin >> u;

        g[u].push_back(i);

        g[i].push_back(u);

    }

    dfs(1, 0);

    cout << f[1] << endl;

}

signed main(void)

{

    Zeoy;

    int T = 1;

    cin >> T;

    while (T--)

    {

        solve();

    }

    return 0;

}

E. Goose, Goose, DUCK?

给定数组\(a\)，求有多少个不同区间，这些区间中每个不同数出现的次数不为\(k\)次，求出这些不同的区间数

题解：线段树维护最小值和最小值数

我们可以考虑初始为空数组，对于我们每次加入的数，我们将它看成右端点\(r\)，我们要找出对于当前右端点\(r\)来说\([1,r-1]\)中存在多少个合法的左端点\(l\)（合法：区间\([l,r]\)中每个不同数出现的次数不为\(k\)次），我们在模拟时发现对于任意元素\(x\)在\([1,r]\)出现的位置\(p_1,p_2,p_3...p_m，m>=k\)，那么对于这个数\(x\)而言不合法的区间为\([p_{m-k}+1,p_{m-k+1}]\),并且我们发现每次在添加一个新的数\(x\)进入数组后，如果原本\(x\)在\([1,r]\)出现的最后位置\(p_m且m>=k\)，那么会撤销\(x\)之前的不合法区间，产生新的不合法区间

例如\(1,2,2,k=2\),现在对于2来说不合法区间为\([1,2]\),如果我们再添加一个2后,数组变为\(1,2,2,2,k=2\)，那么现在\([1,2]\)变成了合法区间，产生了新的不合法区间\([3,3]\)，所以我们可以把问题简化为撤销不合法区间看作区间\(-1\)，产生新的合法区间看成区间\(+1\)，然后答案即为\(0\)的数量

所以我们只需要使用线段树维护最小值和最小值的个数，然后如果区间的最小值为0，我们对答案就可以加上这段区间最小值0的个数；同时对于任意元素\(x\)出现的位置和个数我们可以利用邻接表的思想实现

#include <bits/stdc++.h>

#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)

#define debug(x) cerr << #x << '=' << x << endl

#define all(x) (x).begin(), (x).end()

#define rson id << 1 | 1

#define lson id << 1

#define int long long

#define mpk make_pair

#define endl '\n'

using namespace std;

typedef unsigned long long ULL;

typedef long long ll;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

const int inf = 0x3f3f3f3f;

const ll INF = 0x3f3f3f3f3f3f3f3f;

const int mod = 1e9 + 7;

const double eps = 1e-9;

const int N = 1e6 + 10, M = 4e5 + 10;

int n, k;

int a[N];

vector<int> v[N];

struct info

{

    int cnt;

    int minn;

};

struct node

{

    int lazy, len;

    info val;

} seg[N << 2];

info operator+(const info &a, const info &b)

{

    info c;

    c.minn = min(a.minn, b.minn);

    c.cnt = 0;

    if (c.minn == a.minn)

        c.cnt += a.cnt;

    if (c.minn == b.minn)

        c.cnt += b.cnt;

    return c;

}

void settag(int id, int tag)

{

    seg[id].val.minn += tag;

    seg[id].lazy += tag;

}

void up(int id)

{

    seg[id].val = seg[id << 1].val + seg[id << 1 | 1].val;

}

void down(int id)

{

    if (seg[id].lazy == 0)

        return;

    settag(id << 1, seg[id].lazy);

    settag(id << 1 | 1, seg[id].lazy);

    seg[id].lazy = 0;

}

void build(int id, int l, int r)

{

    seg[id].len = r - l + 1;

    if (l == r)

    {

        seg[id].val.minn = 0;

        seg[id].val.cnt = 1;

        seg[id].lazy = 0;

        return;

    }

    int mid = (l + r) >> 1;

    build(id << 1, l, mid);

    build(id << 1 | 1, mid + 1, r);

    up(id);

}

void modify(int id, int l, int r, int ql, int qr, int val)

{

    if (ql <= l && r <= qr)

    {

        settag(id, val);

        return;

    }

    down(id);

    int mid = (l + r) >> 1;

    if (qr <= mid)

        modify(id << 1, l, mid, ql, qr, val);

    else if (ql > mid)

        modify(id << 1 | 1, mid + 1, r, ql, qr, val);

    else

    {

        modify(id << 1, l, mid, ql, qr, val);

        modify(id << 1 | 1, mid + 1, r, ql, qr, val);

    }

    up(id);

}

info query(int id, int l, int r, int ql, int qr)

{

    if (ql <= l && r <= qr)

    {

        return seg[id].val;

    }

    down(id);

    int mid = (l + r) >> 1;

    if (qr <= mid)

        return query(id << 1, l, mid, ql, qr);

    else if (ql > mid)

        return query(id << 1 | 1, mid + 1, r, ql, qr);

    else

        return query(id << 1, l, mid, ql, qr) + query(id << 1 | 1, mid + 1, r, ql, qr);

}

void solve()

{

    cin >> n >> k;

    for (int i = 1; i <= n; ++i)

        cin >> a[i];

    build(1, 1, n);

    int ans = 0;

    for (int i = 1; i <= n; ++i)

    {

        if (v[a[i]].size() >= k)

        {

            int l, r;

            if (v[a[i]].size() == k)

                l = 1, r = v[a[i]][v[a[i]].size() - k];

            else

            {

                l = v[a[i]][v[a[i]].size() - k - 1] + 1;

                r = v[a[i]][v[a[i]].size() - k];

            }

            // cout << l << ' ' << r << endl;

            modify(1, 1, n, l, r, -1);

        }

        v[a[i]].push_back(i);

        if (v[a[i]].size() >= k)

        {

            int l, r;

            if (v[a[i]].size() == k)

                l = 1, r = v[a[i]][v[a[i]].size() - k];

            else

            {

                l = v[a[i]][v[a[i]].size() - k - 1] + 1;

                r = v[a[i]][v[a[i]].size() - k];

            }

            modify(1, 1, n, l, r, 1);

        }

        if (query(1, 1, n, 1, i).minn == 0)

            ans += query(1, 1, n, 1, i).cnt;

    }

    cout << ans << endl;

}

signed main(void)

{

    Zeoy;

    int T = 1;

    // cin >> T;

    while (T--)

    {

        solve();

    }

    return 0;

}

K. Maximum GCD

给定一个长度为\(n\)的数组，如果这个数组中所有元素的\(gcd\)越大，那么这个数组就越漂亮，现在可以进行任意次操作，每次操作可以对任意一个元素进行取模，然后使得最后数组\(gcd\)最大，并求出最大\(gcd\)

题解：思维

引理：对于任意数\(x\)进行取模，如果\(x\)是偶数，那么\(x\)取模后为\([0,x/2-1]\),如果\(x\)是奇数，那么\(x\)取模后为\([0,x/2]\)

我们发现\(gcd\)最大值小于等于该数组中最小元素\(x\)，

  1. 如果所有的数取模后的范围中都包含\(x\)，那么最大值一定是\(x\)
  2. 如果所有数都是\(x\)的倍数，那么最大值也一定是\(x\)
  3. 如果不是以上情况那么最后答案一定是\(\lfloor \frac{x}{2} \rfloor\)
#include <bits/stdc++.h>

#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)

#define debug(x) cerr << #x << '=' << x << endl

#define all(x) (x).begin(), (x).end()

#define rson id << 1 | 1

#define lson id << 1

#define int long long

#define mpk make_pair

#define endl '\n'

using namespace std;

typedef unsigned long long ULL;

typedef long long ll;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

const int inf = 0x3f3f3f3f;

const ll INF = 0x3f3f3f3f3f3f3f3f;

const int mod = 1e9 + 7;

const double eps = 1e-9;

const int N = 2e5 + 10, M = 4e5 + 10;

int n;

void solve()

{

    cin >> n;

    vector<int> a;

    for (int i = 1; i <= n; ++i)

    {

        int x;

        cin >> x;

        a.push_back(x);

    }

    sort(all(a));

    int minn = INF;

    bool flag = true;

    for (int i = 1; i < a.size(); ++i)

    {

        if (a[i] % a[0] != 0)

            flag = false;

        minn = min(a[i] / 2, minn);

    }

    if (minn >= a[0] || flag == true)

        cout << a[0] << endl;

    else

    {

        cout << a[0] / 2 << endl;

    }

}

signed main(void)

{

    Zeoy;

    int T = 1;

    // cin >> T;

    while (T--)

    {

        solve();

    }

    return 0;

}

L. Permutation Compression

给定一个排列\(a\)，通过执行\(k\)次以下操作回答是否可以将其转换为另一个序列\(b\)，每次可以选择一个长度为\(l_i\)的区间并删除该区间中的最大元素

题解：贪心 + \(set\)动态维护左右两边最大值 + 树状数组计数

经过模拟我们发现我们可以贪心的在排列\(a\)中从大到小删除元素，我们发现一个数\(x\)如果能被当成最大值被删除的区间为\(x\)左边第一个比\(x\)大的数的位置和\(x\)右边第一个比\(x\)大的数的位置形成的区间\([max_l,max_r]\),但是我们不能用单调栈实现，因为整个删除过程是动态的，所以我们考虑利用\(set\)动态维护\(x\)左右两边最大值的位置（因为我们是从大到小删除元素的，所以对于\(x\)来说，如果比\(x\)大的元素没有被删除，那么它的位置一定会出现在\(set\)中，那么对于\(x\)来说，我们就可以利用\(set\)二分出比\(x\)大的元素的位置形成区间\([max_l,max_r]\)），我们只要利用树状数组计算出在这个区间中一共有多少个未被删除的数即可，这样就动态维护出了\(x\)作为最大值所在区间的长度\(len\)，\(len\)即为该区间中未被删除的数，然后如果给定的操作中存在\(l_i <= len\)，代表有操作可以实现删除\(x\)，反之则代表无法还原成序列\(b\)

存在许多边界，比较难调，重点了解思路

#include <bits/stdc++.h>

#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)

#define debug(x) cerr << #x << '=' << x << endl

#define all(x) (x).begin(), (x).end()

#define rson id << 1 | 1

#define lson id << 1

#define int long long

#define mpk make_pair

#define endl '\n'

using namespace std;

typedef unsigned long long ULL;

typedef long long ll;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

const int inf = 0x3f3f3f3f;

const ll INF = 0x3f3f3f3f3f3f3f3f;

const int mod = 1e9 + 7;

const double eps = 1e-9;

const int N = 2e5 + 10, M = 4e5 + 10;

int n, m, k;

int a[N], b[N];

int pos[N];

int c[N];

multiset<int> st;

int lowbit(int x)

{

    return x & -x;

}

void add(int x, int val)

{

    while (x <= n)

    {

        c[x] += val;

        x += lowbit(x);

    }

}

int getsum(int x)

{

    int sum = 0;

    while (x > 0)

    {

        sum += c[x];

        x -= lowbit(x);

    }

    return sum;

}

void solve()

{

    st.clear();

    cin >> n >> m >> k;

    vector<int> vis(n + 10);

    for (int i = 1; i <= n; ++i)

        c[i] = 0;

    for (int i = 1; i <= n; ++i)

    {

        cin >> a[i];

        pos[a[i]] = i;

    }

    for (int i = 1; i <= m; ++i)

    {

        cin >> b[i];

        vis[b[i]] = 1;

    }

    for (int i = 1; i <= k; ++i)

    {

        int len;

        cin >> len;

        st.insert(len);

    }

    for (int i = 1, j = 1; i <= m; ++i)

    {

        while (j <= n && a[j] != b[i])

            j++;

        if (j > n)

        {

            cout << "NO" << endl;

            return;

        }

    }

    for (int i = 1; i <= n; ++i)

        add(i, 1);

    set<int> st2;

    st2.insert(0);

    st2.insert(n + 1);

    for (int i = n; i >= 1; i--)

    {

        if (vis[i])

        {

            st2.insert(pos[i]);

            continue;

        }

        auto it2 = st2.lower_bound(pos[i]);

        int l = *(prev(it2)), r = *it2;

        int len = getsum(r - 1) - getsum(l);

        add(pos[i], -1);

        auto it = st.upper_bound(len);

        if (it == st.begin())

        {

            cout << "NO" << endl;

            return;

        }

        st.erase(--it);

    }

    cout << "YES" << endl;

}

signed main(void)

{

    Zeoy;

    int T = 1;

    cin >> T;

    while (T--)

    {

        solve();

    }

    return 0;

}

The 2023 ICPC Asia Hong Kong Regional Programming Contest的更多相关文章

  1. 2019-2020 ICPC Asia Hong Kong Regional Contest

    题解: https://files.cnblogs.com/files/clrs97/19HKEditorial-V1.zip Code:(Part) A. Axis of Symmetry #inc ...

  2. 2019-2020 ICPC Asia Hong Kong Regional Contest J. Junior Mathematician 题解（数位dp）

    题目链接 题目大意 要你在[l,r]中找到有多少个数满足\(x\equiv f(x)(mod\; m)\) \(f(x)=\sum_{i=1}^{k-1} \sum_{j=i+1}^{k}d(x,i) ...

  3. Asia Hong Kong Regional Contest 2016

    A. Colourful Graph 可以在$2n$步之内实现交换任意两个点的颜色,然后就可以构造出方案. #include <bits/stdc++.h> using namespace ...

  4. Asia Hong Kong Regional Contest 2019

    A. Axis of Symmetry B. Binary Tree n 的奇偶性决定胜负. C. Constructing Ranches 路径上点权之和大于,极大值两倍,这是路径上点能拼出多边形的 ...

  5. 2017-2018 ACM-ICPC Latin American Regional Programming Contest PART （11/13）

    $$2017-2018\ ACM-ICPC\ Latin\ American\ Regional\ Programming\ Contest$$ \(A.Arranging\ tiles\) \(B. ...

  6. 2017-2018 ACM-ICPC Southeastern European Regional Programming Contest (SEERC 2017)

    2017-2018 ACM-ICPC Southeastern European Regional Programming Contest (SEERC 2017) 全靠 wxh的博客 补完这套.wx ...

  7. 2018-2019 ACM-ICPC Southeastern European Regional Programming Contest (SEERC 2018)

    layout: post title: 2018-2019 ACM-ICPC Southeastern European Regional Programming Contest (SEERC 201 ...

  8. 训练20191007 2017-2018 ACM-ICPC Latin American Regional Programming Contest

    2017-2018 ACM-ICPC Latin American Regional Programming Contest 试题地址:http://codeforces.com/gym/101889 ...

  9. 2020 ICPC Universidad Nacional de Colombia Programming Contest

    2020 ICPC Universidad Nacional de Colombia Programming Contest A. Approach 三分 显然答案可以三分,注意\(eps\)还有两条 ...

  10. Hong Kong Regional Online Preliminary 2016 C. Classrooms

    Classrooms 传送门 The new semester is about to begin, and finding classrooms for orientation activities ...

随机推荐

  1. 深入理解c语言指针与内存

    一.将int强制转换为int指针,将int指针强转换为int void f(void) { int *p = (int*)100; //将int强制转换为int指针 printf("%d\n ...

  2. UC_Center整合单点登录后远程注册不激活问题的解决办法

    修改:bbs目录\uc_server\model\user.php 下方法add_user 如下: function add_user($username, $password, $email, $u ...

  3. 深度学习Python代码小知识点(备忘，因为没有脑子)

    现在是2024年4月24日16:58,今天摸鱼有点多,备忘一下,都写到一篇内容里面,免得分散. 1. np.concatenate()函数'np.concatenate'是NumPy库中用来合并两个或 ...

  4. AI老照片修复神器，Anole下载介绍

    最近AI老照片修复上色,再一次火出圈,一些社交平台关于此话题内容流量满满,尤其是在小红书和抖音火的不得了,本期文章就来给大家分享下AI修复老照片的方式方法 本文主要介绍使用Anole修复老照片的方法, ...

  5. Python条件语句 if

    语法: 示例: if elif else:

  6. springboot整合shiro框架详解

    在ShiroRealm 中 对所有 引入的service 加上注解 @Lazy ,防止 事务回滚失败.具体原因看该文章 新增整合swagger2,因为之前整合了shiro,所以再访问swagger的时 ...

  7. php获取支付宝用户信息

    php获取支付宝用户信息 一:创建应用 要在您的应用中使用支付宝开放产品的接口能力: 您需要先去蚂蚁金服开放平台(open.alipay.com),在开发者中心创建登记您的应用,此时您将获得应用唯一标 ...

  8. ftrace在应用上的使用

    之前介绍通过命令行配置和使用ftrace功能,但是实际中,我们也会希望抓C/C++程序中某段代码的调度情况.笔者前不久就遇到这种问题,某个函数调用时延概率超过100ms,是为什么?这时候就需要在他们代 ...

  9. Android dtbo(3) 编译和验证

    您可以使用设备树编译器 (DTC) 编译设备树源文件.不过,在将叠加层 DT 应用于目标主 DT 之前,您还应该通过模拟 DTO 的行为来验证结果. 1. 通过DTC进行编译 构建主 DT .dts ...

  10. 宝塔部署java后端项目

    1. 安装插件 宝塔面板找到软件商店然后搜索 Java java项目管理安装 安装后点击设置准备安装 tomcat 2. 添加项目