3.14 + 1e10 - 1e10 = 0 ? ——浮点数的本质

3.14 + 1e10 - 1e10 = 0 ? ——浮点数的本质

我们先看这样一个例子：

#include <iostream>

int main(int argc, char **argv)
{   

    float a = 3.14;
    float b = 1e10;

    std::cout <<  a << "   " <<  b << std::endl;
    std::cout <<  (a+b)-b << std::endl;
    std::cout <<  a+(b-b) << std::endl;

	return 0;
}

这个程序的输出是：

我们可以看到 (a+b)-b 得到了0，这个结果是有些匪夷所思的。为了解答这个问题，我们需要理解浮点数在计算机中的表示方法。

浮点数的表示——IEEE754

IEEE浮点标准使用\(V = (-1)^s \times M \times 2^E\)来表示一个数，其中\(s\)是一个符号位，取0或者1，用来确定实数的符号，\(M\)是尾数，\(E\)是阶码，通常用移码表示。

对于单精度浮点数，符号位为1位，阶码为8位，尾数为23位。对于双精度浮点数，符号位为1位，阶码为11位，尾数为52位。

举个例子，对于一个实数0.675，其二进制表示为0.101，我们可以看做\(（-1）^0 \times 1.01 \times 2^{-1}\)，因此阶码\(E\)的移码表示是10000000，对于尾数，暗含一个1，因此对于尾数的表示是01000000000000000000000，空余位补0，综上可以得到0.625的单精度浮点数表示：

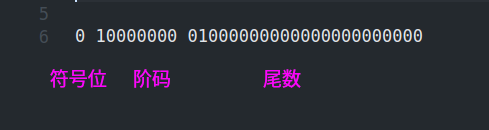
这里帮大家回顾一下浮点数的表示，更多细节可以查阅相关资料。

现在我们就可以回答上面的问题了:

\[1e10 = 10000000000 = 1001010100000010111110010000000000_2 = 1.001010100000010111110010000000000_2 \times 2^{33}
\]

此时1e10二进制表示的尾数部分是高于23位的，因此会执行舍入操作，因此尾数\(M\)=00101010000001011111001。

综上，1e10的单精度浮点数表示是： 0 101000 00101010000001011111001。

而对于3.14则有：\(3.14 \approx 11.0010001111010111000010100011110_2 =1.10010001111010111000010100011110_2 \times 2^1\)

为了实现3.14+1e20，我们需要调整3.14的阶码，使得二者的阶码相同

因此此时有：

\[3.14 \approx
\\ 0.00000000000000000000000000000000110010001111010111000010100011110_2 \times 2^{33}
\]

二者相加有，\(3.14+1e20 = 1.00101010000001011111001（截断）000000000110010001111010111000010100011110_2 \times 2^{33}\)

由于单精度浮点数尾数只有23位，因此会进行舍入操作，这里是截断23位之后的二进制数字，最终3.14+1e10与1e10的二进制代码相同，

所以(3.14 + 1e10) -1e10 = 0

扩展

1. 回到最开始的代码，如果将a，b修改为double类型，得到的结果是不是会有变化呢？

​ 答案是会的，因此double的尾数是52位，因此尾数并不会发生舍入，所以此时的结果是正确的。

1. 我们可以发现，当浮点数a >> b时，由于需要调整b的阶码与a对齐，所以a的尾数表示左侧可能会出现大量的0，导致b的有效位被截断而丢失。