【刚度矩阵推导】2d frame 单元

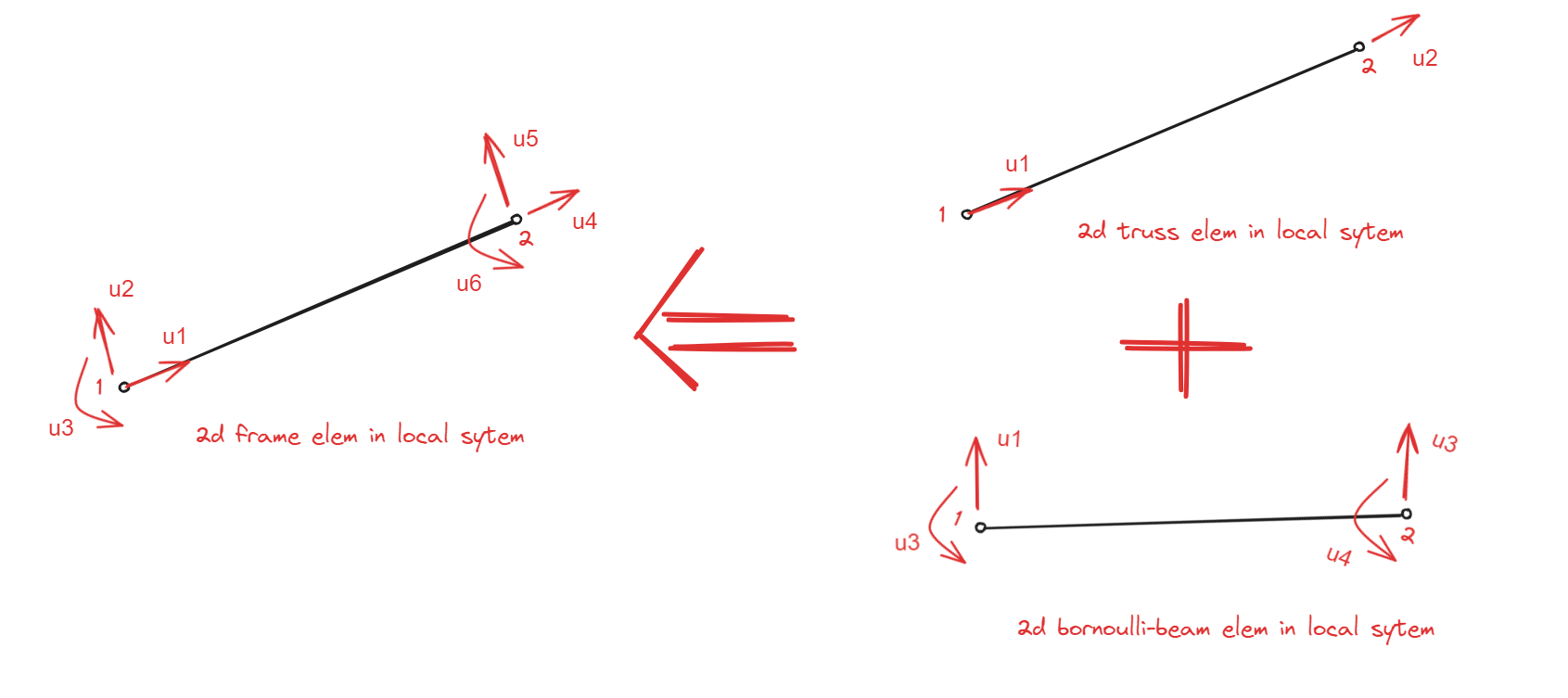
2d frame 单元是x-y平面上的单元,每个节点上有2个平移自由度的和一个转动自由度.局部坐标系下,单元位移向量为:

\(
u=[ u_1 ,u_2 ,u_3, u_4, u_5, u_6]^{T}
\)

其局部坐标系下的刚度矩阵可以由2d truss单元和2d bornoulli-beam单元的刚度矩阵组合而成.

使用matlab进行推导:

% ! bornoulli-beam element stiffness matrix in local system
clc
clear

syms E Iz L A

a=0.5*L;

k_e_bornoulli_beam_stiffness=E*Iz/(2*a^3)*[3 3*a -3 3*a ;3*a 4*a*a -3*a 2*a*a; -3 -3*a 3 -3*a;3*a 2*a*a -3*a 4*a*a ];
disp('k_e_bornoulli_beam_stiffness:')
simplify(k_e_bornoulli_beam_stiffness)

% todo : 2d truss element stiffness matrix in local system

k_e_2d_truss_stiffness=(E*A/L)*[1 -1; -1 1];

% todo : elem's dof
frame_2d_stiffness=sym(zeros(6,6));

frame_2d_stiffness([1,4],[1,4])=k_e_2d_truss_stiffness;

frame_2d_stiffness([2,3,5,6],[2,3,5,6])=k_e_bornoulli_beam_stiffness;
disp('frame_2d_stiffness:')
simplify(frame_2d_stiffness)

<!-- 输出结果 -->

k_e_bornoulli_beam_stiffness:

[ (12*E*Iz)/L^3,  (6*E*Iz)/L^2, -(12*E*Iz)/L^3,  (6*E*Iz)/L^2]
[  (6*E*Iz)/L^2,    (4*E*Iz)/L,  -(6*E*Iz)/L^2,    (2*E*Iz)/L]
[-(12*E*Iz)/L^3, -(6*E*Iz)/L^2,  (12*E*Iz)/L^3, -(6*E*Iz)/L^2]
[  (6*E*Iz)/L^2,    (2*E*Iz)/L,  -(6*E*Iz)/L^2,    (4*E*Iz)/L]

frame_2d_stiffness:

[ (A*E)/L,              0,             0, -(A*E)/L,              0,             0]
[       0,  (12*E*Iz)/L^3,  (6*E*Iz)/L^2,        0, -(12*E*Iz)/L^3,  (6*E*Iz)/L^2]
[       0,   (6*E*Iz)/L^2,    (4*E*Iz)/L,        0,  -(6*E*Iz)/L^2,    (2*E*Iz)/L]
[-(A*E)/L,              0,             0,  (A*E)/L,              0,             0]
[       0, -(12*E*Iz)/L^3, -(6*E*Iz)/L^2,        0,  (12*E*Iz)/L^3, -(6*E*Iz)/L^2]
[       0,   (6*E*Iz)/L^2,    (2*E*Iz)/L,        0,  -(6*E*Iz)/L^2,    (4*E*Iz)/L]