复化梯形求积分——用Python进行数值计算

　　用程序来求积分的方法有很多，这篇文章主要是有关牛顿-科特斯公式。

　　学过插值算法的同学最容易想到的就是用插值函数代替被积分函数来求积分，但实际上在大部分场景下这是行不通的。

　　插值函数一般是一个不超过n次的多项式，如果用插值函数来求积分的话，就会引进高次多项式求积分的问题。这样会将原来的求积分问题带到另一个求积分问题：如何求n次多项式的积分，而且当次数变高时，会出现龙悲歌现象，误差反而可能会增大，并且高次的插值求积公式有可能会变得不稳定：详细原因不赘述。

　　牛顿-科特斯公式解决这一问题的办法是将大的插值区间分为一堆小的插值区间，使得多项式的次数不会太高。然后通过引入参数函数

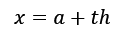
将带有幂的项的取值范围固定在一个固定范围内，这样一来就将多项式带有幂的部分的求积变为一个固定的常数，只需手工算出来即可。这个常数可以直接带入多项式求积函数。

　　上式中x的求积分区间为[a, b]，h = (b - a)/n, 这样一来积分区间变为[0， n]，需要注意的是从这个公式可以看出一个大的区间被分为n个等长的小区间。 这一部分具体请参见任意一本有关数值计算的书！

　　 n是一个事先确定好的值。

　　又因为一个大的插值区间需要被分为等长的多个小区间，并在这些小区间上分别进行插值和积分，因此此时的牛顿-科特斯公式被称为：复化牛顿-科特斯公式。

　　 并且对于n的不同取值牛顿-科特斯有不同的名称： 当n=1时，叫做复化梯形公式，复化梯形公式也就是将每一个小区间都看为一个梯形（高为h，上底为f(t), 下底为f(t+1)）。这与积分的本质：无限分隔  相同。

　　当n=2时，复化牛顿-科特斯公式被称为复化辛普森公式（非美国法律界著名的那个辛普森）。

　　我这篇文章实现的是复化梯形公式：

　　　　

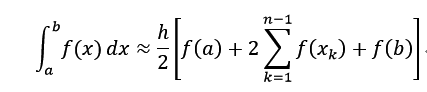
　　首先写一个函数求节点函数值求和那部分：

　　　　

"""
@brief: 求和 ∑f(xk) : xk表示等距节点的第k个节点，不包括端点
        xk = a + kh (k = 0, 1, 2, ...)
        积分区间为[a, b]

@param: xk      积分区间的等分点x坐标集合（不包括端点）
@param: func    求积函数
@return: 返回值为集合的和
"""
def sum_fun_xk(xk, func):
    return sum([func(each) for each in xk])

　　

　　然后就可以写整个求积分函数了：

"""
@brief: 求func积分 :

@param: a  积分区间左端点
@param: b  积分区间右端点
@param: n  积分分为n等份（复化梯形求积分要求）
@param: func  求积函数
@return: 积分值
"""
def integral(a, b, n, func):
    h = (b - a)/float(n)
    xk = [a + i*h for i in range(1, n)]
    return h/2 * (func(a) + 2 * sum_fun_xk(xk, func) + func(b))

　　相当的简单

　　

　　试验：

　　当把大区间分为两个小区间时：

　　　　

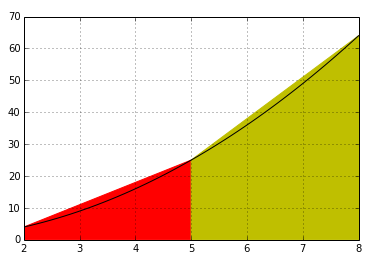
　　分为20个小区间时：

　　

　　求的积分值就是这些彩色的梯形面积之和。

　　测试代码：

if __name__ == "__main__":

    func = lambda x: x**2
    a, b = 2, 8
    n = 20
    print integral(a, b, n, func)

    ''' 画图 '''
    import matplotlib.pyplot as plt
    plt.figure("play")
    ax1 = plt.subplot(111)
    plt.sca(ax1)

    tmpx = [2 + float(8-2) /50 * each for each in range(50+1)]
    plt.plot(tmpx, [func(each) for each in tmpx], linestyle = '-', color='black')

    for rang in range(n):
        tmpx = [a + float(8-2)/n * rang, a + float(8-2)/n * rang, a + float(8-2)/n * (rang+1), a + float(8-2)/n * (rang+1)]
        tmpy = [0, func(tmpx[1]), func(tmpx[2]), 0]
        c = ['r', 'y', 'b', 'g']
        plt.fill(tmpx, tmpy, color=c[rang%4])
    plt.grid(True)
    plt.show()

　　注意上面代码中的n并不是上文开篇提到的公式中的n，开篇提到的n是指将每一个具体的插值区间（也就是小区间）等距插n个节点，复化梯形公式的n是固定的为1.

　　而代码中的n指将大区间分为n个小区间。