BZOJ2591/LG3047 「USACO12FEB」Nearby Cows 换根树形DP

问题描述

BZOJ2591

LG3047

---

题解

换根树形DP。

设 \(opt[i][j]\) 代表 当 \(1\) 为根时，\(i\) 为根的子树中，到 \(i\) 的距离为 \(j\) 的权值和 。

此时我们就可以得到 \(1\) 号结点的答案。

考虑这样做 \(n\) 遍，可以求出答案，但是会T飞掉。

观察每次暴力DP，发现大部分结点的信息还是相同的，这是优化复杂度的关键所在。

考虑换根。

从 \(x\) 号结点转移到 \(y\) 号节点上，发现只有 \(x,y\) 两个结点的信息被改变了。

换根后

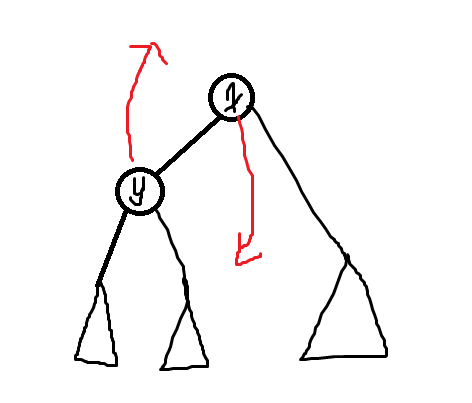
只要将 \(y\) 结点距离 \(p\) 加上 \(x\) 结点距离 \(p-1\) 的信息就行了。

但是发现 \(x\) 号结点距离 \(p-1\) 的信息中，还包含 \(y\) 号结点 \(p-2\) 的信息，所以要倒序枚举 \(p\) ，去重。

---

\(\mathrm{Code}\)

#include<bits/stdc++.h>
using namespace std;

template <typename Tp>
void read(Tp &x){
	x=0;char ch=1;int fh;
	while(ch!='-'&&(ch>'9'||ch<'0')) ch=getchar();
	if(ch=='-') ch=getchar(),fh=-1;
	else fh=1;
	while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
	x*=fh;
}

const int maxn=100007;
const int maxm=200007;

int n,k;
int Head[maxn],to[maxm],Next[maxm],tot;
int c[maxn];

void add(int x,int y){
	to[++tot]=y,Next[tot]=Head[x],Head[x]=tot;
}

int opt[maxn][21];

void dp(int x,int f){
	opt[x][0]=c[x];
	for(int i=Head[x];i;i=Next[i]){
		int y=to[i];
		if(y==f) continue;
		dp(y,x);
		for(int j=1;j<=k;j++){
			opt[x][j]+=opt[y][j-1];
		}
	}
}

int ans[maxn];

void calc(int x,int y){
	for(int i=k;i>=2;i--) opt[y][i]+=opt[x][i-1]-opt[y][i-2];
	opt[y][1]+=opt[x][0];
}

void zy(int x,int f){
	for(int i=0;i<=k;i++) ans[x]+=opt[x][i];
	for(int i=Head[x];i;i=Next[i]){
		int y=to[i];
		if(y==f) continue;
		calc(x,y);zy(y,x);
	}
}

int main(){
	read(n);read(k);
	for(int i=1,x,y;i<n;i++){
		read(x);read(y);
		add(x,y);add(y,x);
	}
	for(int i=1;i<=n;i++) read(c[i]);
	dp(1,0);zy(1,0);
	for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
	return 0;
}