luogu P3830 [SHOI2012]随机树

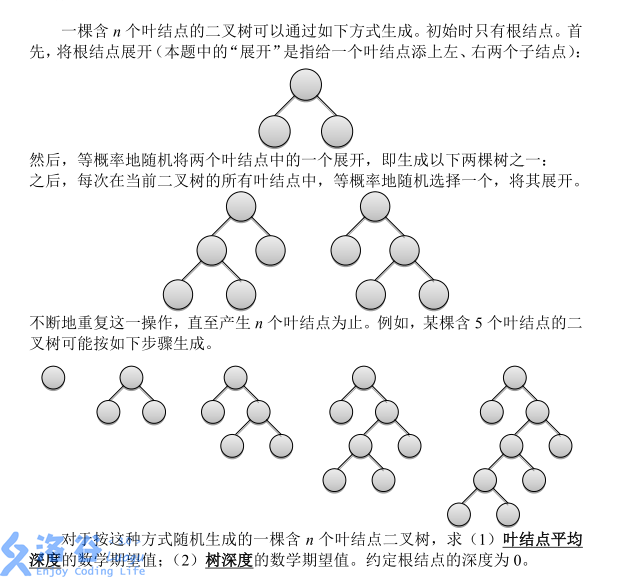
输入格式

输入仅有一行，包含两个正整数 q, n，分别表示问题编号以及叶结点的个数。

输出格式

输出仅有一行，包含一个实数 d，四舍五入精确到小数点后 6 位。如果 q = 1，则 d 表示叶结点平均深度的数学期望值；如果 q = 2，则 d 表示树深度的数学期望值。

---

p=1

令f(x)表示有x个叶子节点的树的叶子节点平均深度,则

f(x)*x 为叶子节点深度之和

f(x)+2随机选择一个叶子节点展开后增加的深度

f(x)= ((x-1)f(x-1)+f(x-1)+2)/x = (xf(x) +2)/x = f(x) + 2/x

---

p=2:

设f[i][j]表示当一颗树有i个叶子节点，且深度大于等于j时的概率； 设p[i][j]表示当一颗树有i个叶子节点，且深度等于jj​时的概率；

则有f[i][j]=p[i][j]+p[i][j+1]+⋯+p[i][n−1]

f[n][1]=\(\sum_{i=1}^{n-1}\)p[n][i]

f[n][2]=\(\sum_{i=2}^{n-1}\)p[n][i]

f[n][3]=\(\sum_{i=3}^{n-1}\)p[n][i]

.

.

.

f[n][n-1]=p[n][n-1]

\(\sum_{i=1}^{n-1}\)f[n][i]=\(\sum_{i=1}^{n-1}\)p[n][i]*i

\(\sum_{i=1}^{n-1}\)f[n][i] 即为所求

#include<cstdio>
#include<iostream>
using namespace std;
#define int long long
#define db double
int p,n;
db f[110],dp[110][110],ans;
inline void work(){
	for(int i=1;i<=n;i++)dp[i][0]=1;
	for(int i=2;i<=n;i++)
	for(int j=1;j<i;j++){
		for(int k=1;k<i;k++)
		dp[i][j]+=dp[k][j-1]+dp[i-k][j-1]-dp[k][j-1]*dp[i-k][j-1];
		dp[i][j]/=(i-1);
	}
	for(int i=1;i<n;i++)ans+=dp[n][i];
	printf("%.6f\n",ans);
}
signed main(){
	cin>>p>>n;
	if(p==1){
		f[1]=0;for(int i=2;i<=n;i++)f[i]=f[i-1]+2.0/i;
		printf("%.6f\n",f[n]);
	}else work();
}