dp递推 hdu1978

How many ways

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5422    Accepted Submission(s): 3185

Problem Description

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

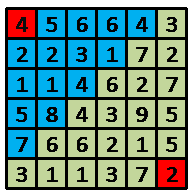
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

Input

第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

 

Sample Output

3948

 

Author

xhd

 

Source

2008杭电集训队选拔赛

 

Recommend

wangye   |   We have carefully selected several similar problems for you:  1421 1789 1159 1176 1257 

 

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 121
int main()
{
    int dp[maxn][maxn],num[maxn][maxn],T,n,m;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
                scanf("%d",&num[i][j]);
        memset(dp,,sizeof(dp));
        dp[][]=;
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=m;j++)
            {
                if(i==n&&j==m)
                    continue;
                dp[i][j] %= ;
                for(int x=i;x<=num[i][j]+i&&x<=n;x++)
                {
                    for(int y=j;y<=num[i][j]+j&&y<=m;y++)
                    {
                        if(x==i&&y==j)
                            continue;
                        if(num[i][j]>=x-i+y-j)
                        {
                            dp[x][y] += dp[i][j];//不断地把前面的得出的方法数加到后面，每一点就代表从起点到这一点的方法数
                        }
                    }
                }
            }
        }
        dp[n][m] %= ;
        printf("%d\n",dp[n][m]);
    }
    return ;
}