NVDLA中Winograd卷积的设计

在AI芯片：高性能卷积计算中的数据复用曾提到，基于变换域的卷积计算——譬如Winograd卷积——并不能适应算法上对卷积计算多变的需求。但Winograd卷积依旧出现在刚刚公开的ARM Ethos-N57和Ethos-N37 NPUs的支持特性中，本文将利用Nvidia开源的NVIDIA Deep Learning Accelerator (NVDLA)为例，分析在硬件中支持Winograd卷积的实现方式，代价和收益；以期对基于变换域卷积的优势和不足有更深的认识。

1. Windgrad卷积的计算方式

卷积神经网络中的三维卷积（后文简称为卷积）计算过程可以表示如下，将这种直接通过原始定义计算卷积的方式称为直接卷积（Direct Convolution）。

for i = 1 : Ho
    for j = 1 : Wo
        for k = 1 : Co
            for l = 1 : R
                for m = 1 : S
                    for n = 1 : Ci
                        out[i,j,k] += In[i*s+l.j*s+m,n]*F[l,m,n];

其中各参数的含义如下表

数据维度	描述
Ho/Wo	输出feature map的高和宽
Co	输出的channel数目
R/S	filter的高和宽
Ci	输入的channel数目
s	卷积计算的stride

和一般的乘加运算不同，卷积计算中有滑窗的过程，充分利用这一点特性可以节约计算过程中的乘法次数。关于Winograd的原理和推导，可以参考https://blog.csdn.net/antkillerfarm/article/details/78769624中的相关内容。此处直接给出3x3, stride=1卷积下Winograd卷积的形式(参见NVDLA Unit)。

\[S = A^T\left[\left(GgG^T\right) \odot \left( C^TdC \right) \right]A
\]

\[g = \begin{bmatrix}
wt_{0,0} & wt_{0,1} & wt_{0,2} \\
wt_{1,0} & wt_{1,1} & wt_{1,2} \\
wt_{2,0} & wt_{2,1} & wt_{2,2}
\end{bmatrix}
\]

\[d = \begin{bmatrix}
x_{0,0} & x_{0,1} & x_{0,2} & x_{0,3}\\
x_{1,0} & x_{1,1} & x_{1,2} & x_{1,3}\\
x_{2,0} & x_{2,1} & x_{2,2} & x_{2,3}\\
x_{3,0} & x_{3,1} & x_{3,2} & x_{3,3}
\end{bmatrix}
\]

\[C = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & -1 & 1 \\
-1& 1 & 1 & 0 \\
0 & 0 & 0 & -1
\end{bmatrix}
\]

\[G = \begin{bmatrix}
1 & 0 & 0 \\
0.5 & 0.5 & 0.5 \\
0.5 & -0.5& 0.5 \\
0 & 0 & 1
\end{bmatrix}
\]

\[A_T = \begin{bmatrix}
1 & 1 & 1 & 0 \\
0 & 1 &-1 &-1
\end{bmatrix}
\]

其中\(g\)是3x3的kernel，\(d\)是4x4的feature map，\(\odot\)表示矩阵对应位置元素相乘。\(s\)表示2x2的卷积结果。矩阵\(C\), \(G\), \(A\)为常量，用于Wingrad卷积中的变换。由于\(C\), \(G\), \(A\)中各元素取值为\(\pm1,\pm0.5\), 因此计算可以通过加减和简单移位得到，认为不需要进行乘法运算。

因此，采用Winograd卷积计算得到4哥输出结果需要16次乘法计算，而直接卷积需要36次乘法计算。但是由于Winograd在变换中加入了加法计算，因此加法次数会有一定增加。注意上述讨论中并没有加入Channel方向，这是因为此处卷积在Channel上实际上依旧退化成了简单的乘加运算，因此无论在变换前后进行Channel方向计算均没有区别。

一段直接卷积和Winograd卷积对比的代码如下所示

import numpy as np
g = np.random.randint(-128,127,(3,3))
d = np.random.randint(-128,127,(4,4))
direct_conv = np.zeros((2,2))
for i in range(2):
    for j in range(2):
        for r in range(3):
            for s in range(3):
                direct_conv[i,j] =  direct_conv[i,j] + d[i+r,j+s]*g[r,s]
C = np.array([[1,0,0,0],[0,1,-1,1],[-1,1,1,0],[0,0,0,-1]])
G = np.array([[1,0,0],[0.5,0.5,0.5],[0.5,-0.5,0.5],[0,0,1]])
AT = np.array([[1,1,1,0],[0,1,-1,-1]])
U = G.dot(g).dot(G.transpose())
V = C.transpose().dot(d).dot(C)
wg_conv = AT.dot(U*V).dot(AT.transpose())
print(direct_conv)
print(wg_conv)

由计算结果可知，两者结果完全一致（如果采用浮点数时可能会有量化误差，但都在合理范围内）

>>> print(direct_conv)
[[-23640.    -51.]
 [-10740.   8740.]]
>>> print(wg_conv)
[[-23640.    -51.]
 [-10740.   8740.]]

2. NVDLA中的的直接卷积

在硬件设计过程中不可能为直接卷积和Winograd卷积分别设计完全独立的计算和控制逻辑，由于直接卷积有计算灵活和适应性强的特点，各类神经网络加速器都有支持。因此，Winograd一定是建立在直接卷积硬件结构基础上的拓展功能。在探究NVDLA中的Winograd卷积设计之前，必须先明确NVDLA中的的直接卷积的计算方式。

Nvidia的相关文档中十分详细的NVDLA计算直接卷积的流程（NVDLA Unit)，其将卷积计算分成了五级（下述描述中，以数值精度为Int16为例）

• Atomic Operation （原子操作，完成16次64次乘法并将其加在一起）
• Stripe Operation （条带操作，完成16次独立的Atomic Operation）
• Block Operation （块操作，完成kernel的R/S方向的累加）
• Channel Operation（通道操作，完成Channel方向计算的累加）
• Group Operation （分组操作，完成一组kernel的全部计算）

NVDLA Unit中给出了可视化的图像用于描述这个过程，这一过程实际上就是卷积的六层循环计算过程的拆解，可以表示如下

for k = 1 : Co/16
    for i = 1 : Ho/4                                // Group Operation
        for j = 1 : Wo/4                            // Group Operation
            for n = 1 : Ci/64                       // Channel Operation
                for l = 1 : R                       // Block Operation
                    for m = 1 : S                   // Block Operation
                        for ii = 1:4                // Strip Operation
                            for ji = 1:4            // Strip Operation
                                for ki = 1：16      // Antomic Operation
                                    for ni = 1：64  // Antomic Block
                                        out[i*4+ii,j*4+jj,k*16+ki] +=
                                        In[(i*4+ii)*s+l.(j*4+jj)*s+m,n*64+ni]*F[l,m,n*64+ni];

其中，Atomic Operation决定了NVDLA乘法阵列的设计。根据设计可以看出，NVDLA有16份完全一致的乘法阵列用于计算16个不同Kernel的乘法；而每个乘法阵列中有64个乘法和一棵64输入的加法树。

计算顺序还一定程度确定了NVDLA的Buffer设计和数据路径设计。在计算直接卷积时，每周期需要128Byte的Feature/Pixel数据，实际上时规则的64Channel的数据；因此在存储时只需要每个Bank上存储64Channel数据，使用时通过MUX选出指定Bank数据即可。在进行结果写回时，每周期需要写回16个Feature数据。由于Winograd卷积使用的Weight可以提前算好，对比直接卷积和Winograd卷积时可以忽略Weight路径。

3. NVDLA中的Winograd卷积

建立在直接卷积的硬件架构上，NVDLA针对Winograd卷积进行了一系列的修改。从计算方式上来说，不再同时计算64个Channel的乘加；从硬件架构上来说，进行了计算修改和数据路径修改。根据NVDLA的设计，Winograd卷积的计算\(S = A^T\left[\left(GgG^T\right) \odot \left( C^TdC \right) \right]A\) 实际上分布在不同的阶段/模块进行。

• $U = GgG^T $是离线预先计算好的
• $V = C^TdC $是在数据路径上计算的
• \(S = A^T\left[ U\odot V\right]A\) 是在计算阵列中计算的

首先考虑计算阵列的设计。NVDLA计算3x3卷积，每次输出2x2共计4个数，计算过程中有4x4的矩阵点乘计算；结合直接卷积中64个乘法计算，Winograd卷积同时计算了4个Channel，共计4x4x4=64次乘法。乘法计算本身没有区别，但在进行加法时，和直接卷积略有不同，用代码可表示为

//direct conv & winograd conv
for i = 1:16
    s1[i] = s0[i*4+0] + s0[i*4+1] + s0[i*4+2] + s0[i*4+3];
//direct conv
for i = 1:8
    s2[i] = s1[i*2+0] + s1[i*2+1];
for i = 1:4
    s3[i] = s2[i*2+0] + s2[i*2+1];
s4[i] = s3[0] + s3[1] + s3[2] + s3[3];
//winograd conv
for i=1:4
    s2_wg[0][i] = s1[i*4+0] + s1[i*4+1] + s1[i*4+2];
    s2_wg[0][i] = s1[i*4+1] - s1[i*4+2] + s1[i*4+3];
s3_wg[0][0] = s2_wg[0][0] + s2_wg[0][1] + s2_wg[0][2];
s3_wg[1][0] = s2_wg[1][0] + s2_wg[1][1] + s2_wg[1][2];
s3_wg[0][1] = s2_wg[0][1] - s2_wg[0][1] - s2_wg[0][2];
s3_wg[1][1] = s2_wg[1][1] - s2_wg[1][1] - s2_wg[1][2];

代码中只有第一级的加法被direct conv和winograd conv完全复用，其他级的加法略有不同。在NVDLA中，加法是使用Wallace Tree完成的，以提高性能降低资源占用。Direct Conv中和Winograd Conv中的后面几级加法还进行了进一步复用。总体来说，从代码上看（参见NV_NVDLA_CMAC_CORE_mac.v），为了支持Winograd卷积

• 加法的第三级中增加了4棵4-2的Wallace Tree Compressor
• 加法的第四级中增加了2棵4-2的Wallace Tree Compressor
• 加法的第五级中增加了2棵6-2的Wallace Tree Compressor
• 增加了一些MUX以direct conv和winograd conv

其次考虑数据路径，包括读取的数据路径和写回的数据路径。对于读取而言，除了需要针对Winograd专门设计取址逻辑和数据选择逻辑，还需要完成$V = C^TdC $的计算；根据文档描述，这一计算过程是在PRA（Pre-addition）中完成的。从代码上看（参见NV_NVDLA_CSC_dl.v）

• 针对Winograd的地址生成增加的控制逻辑可以忽略
• 针对Winograd的数据选择增加数千的寄存器
• PRA采用MENTOR的HLS综合工具实现，共实现了4份，和MAC阵列（1024乘加）对比，此处的计算资源较少

对于写回路径而言，为了完成卷积计算，在乘加后增加了累加器和SRAM，其设计如下图所示(ref. http://nvdla.org/_images/ias_image21_cacc.png)

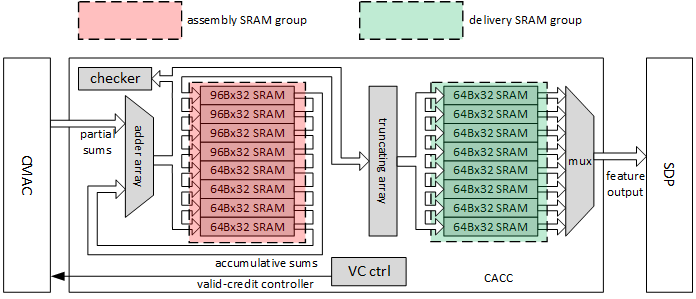
和Direct Conv一次输出16个结果相比，Winograd Conv输出的结果为64。这意味着为了支持Winograd Conv，需要额外增加48组高位宽的累加器。同时，SRAM的大小也需要设置为原先的四倍。

4. 相关讨论

NVDLA为了同时支持Direct Conv和Winograd Conv显然付出了一些代价。定性的分析来看，包括

• 4组PRA，每组PRA中约有8次加法
• 16棵加法树，每棵增加了约8次加法
• 48组高位宽加法
• 增加了约25KB的Accumulator SRAM

而作为对比，一些典型数据包括

• MAC阵列中有1024次乘法和约1024次加法
• 用于存放Feature/Pixel/Weight的Buffer大小为512KB

显然，为了支持Winograd Conv增加的资源并不会太多。当然，虽然读取路径和计算阵列的设计受Winograd Conv的影响不大；但是对于写回路径而言，数据位宽发生了变化，一定程度影响了整体的架构设计。可能可以优化的地方包括将Direct Conv的输出也改成2x2的大小，这样写回的数据路径上Direct Conv和Winograd Conv就没有差别了。

NVDLA是一个相对专用的加速器，从相关文档中也可以看出，NVDLA专门针对计算中的各种特性/数据排列进行了硬件上的处理。而现有的很多加速器，为了兼顾不同网络的计算效率，往往更为灵活。在这种情况下，Winograd Conv应该作为设计的可选项，这是因为

• 计算3x3卷积有2.25x的理论提升
• Winograd Conv的乘法依旧是矩阵计算
• Winograd Conv的数据路径和直接卷积没有必然的冲突
• Winograd Conv的加法可以直接在数据路径上完成，甚至不影响其他设计
• 如果加速器设计粒度足够细，甚至可以从软件调度上直接支持Winograd Conv

完全不考虑Winograd Conv的理由只可能是未来算法发展趋势下，3x3的普通卷积计算量占比会大大下降。

5. 参考

1. NVDLA Documentation
2. NVDLA Soruce Code