LaTex语法

使用LaTex可以生成复杂的数学公式。

举例：

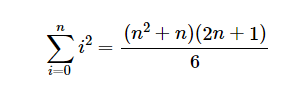
其LaTex语法如下： LaTex具有很强的可读性，例如 sum 表示求和，多练练就能掌握。

 \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6}

LaTex目前已经成为“数理化”的行业的标准语法。因此，你不用担心学会了在其他系统里无法使用。

在word里，你也可以用LaTex语法写公式。

　　

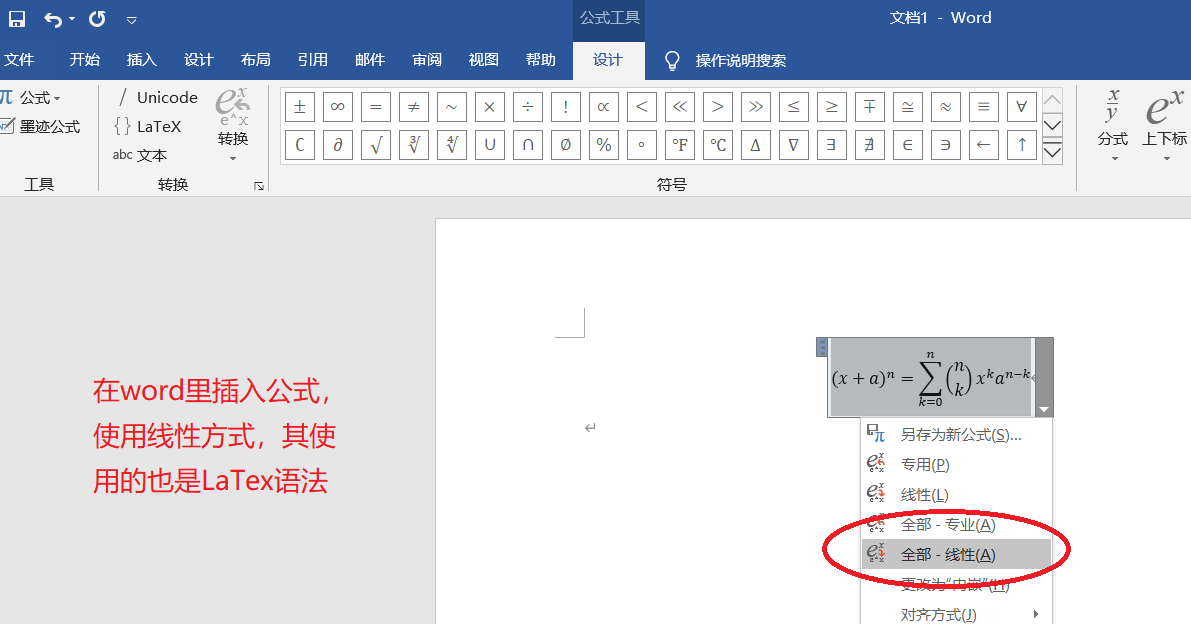
对于部分公式，需要注意：换行。这是因为，部分公式行较高，如果采用行内元素，可能显示错误，请勾选“换行”

 \frac{\partial u}{\partial t}
   = h^2 \left( \frac{\partial^2 u}{\partial x^2}
      + \frac{\partial^2 u}{\partial y^2}
      + \frac{\partial^2 u}{\partial z^2} \right) \

　　

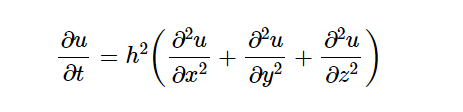
 举例2：

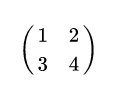
\begin{pmatrix}1&2\\3&4\\ \end{pmatrix}

　　

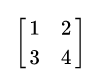
\begin{bmatrix}1&2\\3&4\\ \end{bmatrix}

　　

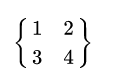
\begin{Bmatrix}1&2\\3&4\\ \end{Bmatrix}

　　

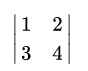
\begin{vmatrix}1&2\\3&4\\ \end{vmatrix}

　　

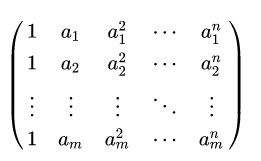
\begin{pmatrix}
 1 & a_1 & a_1^2 & \cdots & a_1^n \\
 1 & a_2 & a_2^2 & \cdots & a_2^n \\
 \vdots  & \vdots& \vdots & \ddots & \vdots \\
 1 & a_m & a_m^2 & \cdots & a_m^n
 \end{pmatrix}

　　

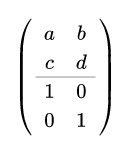
\begin{pmatrix}
    a & b\\
    c & d\\
  \hline
    1 & 0\\
    0 & 1
  \end{pmatrix}

　　

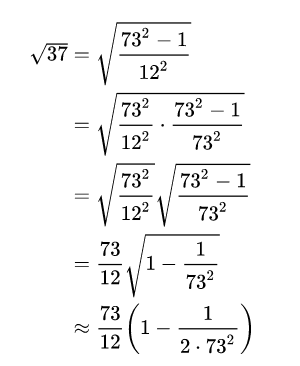
\begin{align}
\sqrt{37} & = \sqrt{\frac{73^2-1}{12^2}} \\
 & = \sqrt{\frac{73^2}{12^2}\cdot\frac{73^2-1}{73^2}} \\
 & = \sqrt{\frac{73^2}{12^2}}\sqrt{\frac{73^2-1}{73^2}} \\
 & = \frac{73}{12}\sqrt{1 - \frac{1}{73^2}} \\
 & \approx \frac{73}{12}\left(1 - \frac{1}{2\cdot73^2}\right)
\end{align}

　　

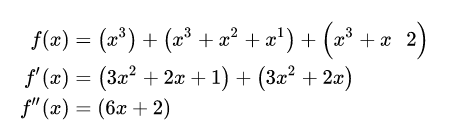
\begin{align} f(x)&=\left(x^3\right)+\left(x^3+x^2+x^1\right)+\left(x^3+x^‌​2\right)\\ f'(x)&=\left(3x^2+2x+1\right)
+
\left(3x^2+2x\right)\\ f''(x)&=\left(6x+2\right)\\ \end{align}

　　

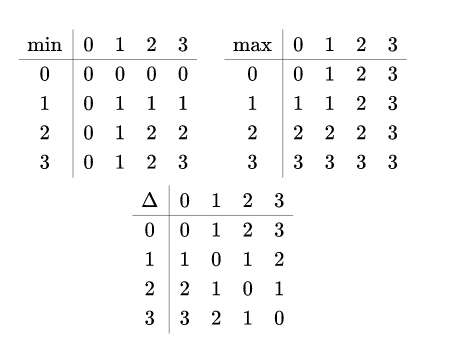
% outer vertical array of arrays
\begin{array}{c}
% inner horizontal array of arrays
\begin{array}{cc}
% inner array of minimum values
\begin{array}{c|cccc}
\text{min} & 0 & 1 & 2 & 3\\
\hline
0 & 0 & 0 & 0 & 0\\
1 & 0 & 1 & 1 & 1\\
2 & 0 & 1 & 2 & 2\\
3 & 0 & 1 & 2 & 3
\end{array}
&
% inner array of maximum values
\begin{array}{c|cccc}
\text{max}&0&1&2&3\\
\hline
0 & 0 & 1 & 2 & 3\\
1 & 1 & 1 & 2 & 3\\
2 & 2 & 2 & 2 & 3\\
3 & 3 & 3 & 3 & 3
\end{array}
\end{array}
\\
% inner array of delta values
\begin{array}{c|cccc}
\Delta&0&1&2&3\\
\hline
0 & 0 & 1 & 2 & 3\\
1 & 1 & 0 & 1 & 2\\
2 & 2 & 1 & 0 & 1\\
3 & 3 & 2 & 1 & 0
\end{array}
\end{array}

　　

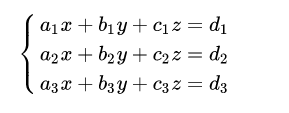
\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{array}
\right.

　　

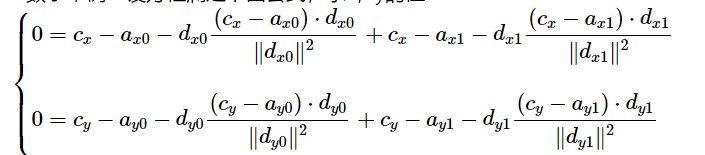
 \left\{ \begin{array}{l}
0 = c_x-a_{x0}-d_{x0}\dfrac{(c_x-a_{x0})\cdot d_{x0}}{\|d_{x0}\|^2} + c_x-a_{x1}-d_{x1}\dfrac{(c_x-a_{x1})\cdot d_{x1}}{\|d_{x1}\|^2} \\[2ex]
0 = c_y-a_{y0}-d_{y0}\dfrac{(c_y-a_{y0})\cdot d_{y0}}{\|d_{y0}\|^2} + c_y-a_{y1}-d_{y1}\dfrac{(c_y-a_{y1})\cdot d_{y1}}{\|d_{y1}\|^2} \end{array} \right.