NP难问题

转自https://blog.csdn.net/u014295667/article/details/47090639

1、首先涉及到的基本概念有：

• （1）确定性算法（Determinism）： 设A是问题Π的一个解决算法，在算法的整个执行过程中，每一步都能得到一个确定的解，这样的算法就是确定性算法。

• （2）非确定性算法（Nondeterminism）：设A是求解问题Π的一个算法，它将问题分解成两部分，分别为猜测阶段和验证阶段，其中

  • 猜测阶段：在这个阶段，对问题的输入实例产生一个任意字符串y，在算法的每一次运行时，串y的值可能不同，因此，猜测以一种非确定的形式工作。
  • 验证阶段：在这个阶段，用一个确定性算法（有限时间内）验证：① 检查在猜测阶段产生的串y是否是合适的形式，如果不是，则算法停下来并得到no；② 如果串y是合适的形式，则验证它是否是问题的解，如果是，则算法停下来并得到yes，否则算法停下来并得到no。它是验证所猜测的解的正确性。

另外涉及到的概念有：

多项式时间（Polynomial）：对于规模为n的输入，它们在最坏的情况下的运行时间为O（n^k）,其中k为某个常数，则该算法为多项式时间的算法
在计算复杂度的理论中，算法的计算时间也就是时间复杂度m（n）不大于算法规模n的多项式倍数，也就是说m(n)是关于n的一个多项式函数。例如，时间复杂度为O（n^2）的就是多项式时间，而时间复杂度为O（2^n）的则不是关于n的多项式函数，因此就不是多项式时间。

　　

2、P类问题，NP类问题，NP难问题，NPC问题

• （1）P类问题：在多项式时间内可解的问题。
• （2）NP类问题（Nondeterminism Polynomial）：在多项式时间内“可验证”的问题。也就是说，不能判定这个问题到底有没有解，而是猜出一个解来在多项式时间内证明这个解是否正确。即该问题的猜测过程是不确定的，而对其某一个解的验证则能够在多项式时间内完成。P类问题属于NP问题，但不确定是否为NP问题的真子集。
• （3）NPC类问题（Nondeterminism Polynomial complete）：存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。其定义要满足2个条件：
  • 首先，它得是一个NP问题；
  • 然后，所有的NP问题都可以约化到它。
• 要证明npc问题的思路就是：
  • 先证明它至少是一个NP问题，
  • 再证明其中一个已知的NPC问题能约化到它。
• （4）NP难问题（NP-hard问题）：NP-Hard问题是这样一种问题，它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比
  NPC问题的范围广，NP-Hard问题没有限定属于NP），即所有的NP问题都能约化到它，但是他不一定是一个NP问题。NP-Hard问题同样难以找到多项式的算法，但它不列入我们的研究范围，因为它不一定是NP问题。即使NPC问题发现了多项式级的算法，NP-Hard问题有可能仍然无法得到多项式级的算法。事实上，由于NP-Hard放宽了限定条件，它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。

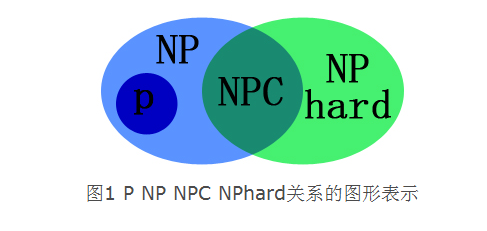
以上四个问题他们之间的关系可以用下图来表示：

3、在2中涉及到的另外一个概念呢，就是：规约/约化

• 简单的说，问题A可以约化为问题B，就可以理解为：问题B的解就一定是问题A的解。
• 也可以理解为，“问题A可归约为问题B”，指问题B的答案可用于解决问题A。因此解决A不会难于解决B。
• 由此也可以知道的是问题B的时间复杂度一定会大于等于问题A。
• 《算法导论》上举了这么一个例子。比如说，现在有两个问题：求解一个一元一次方程和求解一个一元二次方程。那么我们说，前者可以规约为后者，意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题，那么我们能找到一个“规则”，按照这个规则把解一元一次方程程序的输入数据变一下，用在解一元二次方程的程序上，两个程序总能得到一样的结果。这个规则即是：两个方程的对应项系数不变，一元二次方程的二次项系数为0。
• 从规约的定义中我们看到，一个问题规约为另一个问题，时间复杂度增加了，问题的应用范围也增大了。通过对某些问题的不断规约，我们能够不断寻找复杂度更高，但应用范围更广的算法来代替复杂度虽然低，但只能用于很小的一类问题的算法。存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。这种问题的存在难以置信，并且更加不可思议的是，这种问题不只一个，它有很多个，它是一类问题。这一类问题就是传说中的NPC问题，也就是NP-完全问题。