Sparse Filtering简介

当前很多的特征学习(feature learning)算法需要很多的超参数(hyper-parameter)调节, Sparse Filtering则只需要一个超参数--需要学习的特征的个数, 所以非常易于进行参数调节.

1.特征分布及其特性

基本上所有的参数学习算法都是要生成特定的特征分布, 比如sparse coding是要学得一种稀疏的特征, 亦即学到的特征中只有较少的非零项. 基本上所有的特征学习算法都是为了优化特征分布的某些特性的.Sparse Filtering也是这样的一种特征学习方法, 其目的是为了学到拥有一下特定特性的特征, 为了简洁, 首先定义一下符号表示, 令M为特征分布矩阵,每一列列代表一个样本, 每一行代表一个特征(该特征是学到的, 而不是初始的特征), $ f_j^{(i)}$代表矩阵中的第(j,i)项, 亦即第i个样本的第j个特征的激活值 .

1. 每个样本的特征都比较稀疏(Population Sparsity)

每个样本的特征向量中, 只有很少的项是非零的, 亦即M中的每一列都是稀疏的.

2. 每种特征在所有的样本上比较稀疏(Lifetime Sparsity)

每个特征在所有的训练样本上比较稀疏, 亦即M中的每一行都是稀疏的.

3. 特征的分布比较均匀(High Dispersal)

每个特征的统计分布应该是比较接近的, 没有那个特征(亦即M中某行)比其他的特征要稠密的很多. Sparse Filtering使用平均激活平方(mean square activations)来表示特征的分布, 对于特征j, 平均激活平方为$\sum_{i}(f_j^{(i)})^{2}$. Sparse Filtering希望所有的特征的平均激活平方比较接近, 也就意味着所有的特征有着相似的贡献. High Dispersal特性避免了某些特征一直处于激活状态的情况.

特征分布的特性已经在神经科学领域有了一些探索, 并且发现Population Sparsity和Lifetime Sparsity并不一定是相关的. 另外, 除了Sparse Filtering, 许多其他的特征学习方法也会规定这种特征分布的特性. 对于Lifetime Sparsity, Sparse RBM要求特征的平均激活值要接近一个给定的值, ICA和Sparse autoencoder也会规定Lifetime Sparsity. KMeans使用类簇的中心作为特征, 每个样本都只会属于一个类簇, 所以其特征向量中只会有一个非零值, 相当于是Population Sparsity, Sparse Coding也是一种Pupulation Sparsity.

Sparse Filtering直接从特征分布出发, 在满足High Dispersal的条件下优化Population Sparsity, 满足这两个条件的特征也会满足Lifetime Sparsity.

2. Sparse Filtering

令$f_{j}^{(i)}=\boldsymbol{w}_{\boldsymbol{j}}^{T}\boldsymbol{x}^{(i)}$. Sparse Filtering首先对特征分布矩阵M中的每一行进行正则化Z(正则化每一个样本), 然后对每一列进行正则化(正则化每一种特征), 最后优化特征分布矩阵中所有项的绝对值加和. 亦即我们首先正则化特征分布矩阵的每一行:$\tilde{\boldsymbol{f}_{\boldsymbol{j}}}=\boldsymbol{f}_{\boldsymbol{j}}/\|\boldsymbol{f}_{\boldsymbol{j}}\|_2$, 然后正则化特征分布矩阵的每一列:$\hat{\boldsymbol{f}}^{(\boldsymbol{i})}={\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}/\|{\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}\|_2$, 然后优化特征分布矩阵的项的绝对值加权和(假定有n个样本):$$minimize \sum_{i=1}^{n} {\|{\hat{\boldsymbol{f}}}^{(\boldsymbol{i})}\|}_1 = \sum_{i=1}^{n} {\left|\left| \frac{{\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}}{{\|\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}\|_2}\right|\right|}_1$$.

以上算法步骤对于Population Sparsity, Lifetime Sparsity, High Dispersal三种特征特性的优化细节如下:

2.1 对于Population Sparsity的优化:

${\|{\hat{\boldsymbol{f}}}^{(\boldsymbol{i})}\|}_1 = {\left|\left| \frac{{\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}}{{\|\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}\|_2}\right|\right|}_1$衡量了第i个样本的Population Sparsity, 因为正则化后的特征$\hat{\boldsymbol{f}}^{(\boldsymbol{i})}$被限制在一个单位半径的$\ell_2$球上, 最小化${\|{\hat{\boldsymbol{f}}}^{(\boldsymbol{i})}\|}_1$相当于要求样本的特征很稀疏. 如下图所示:

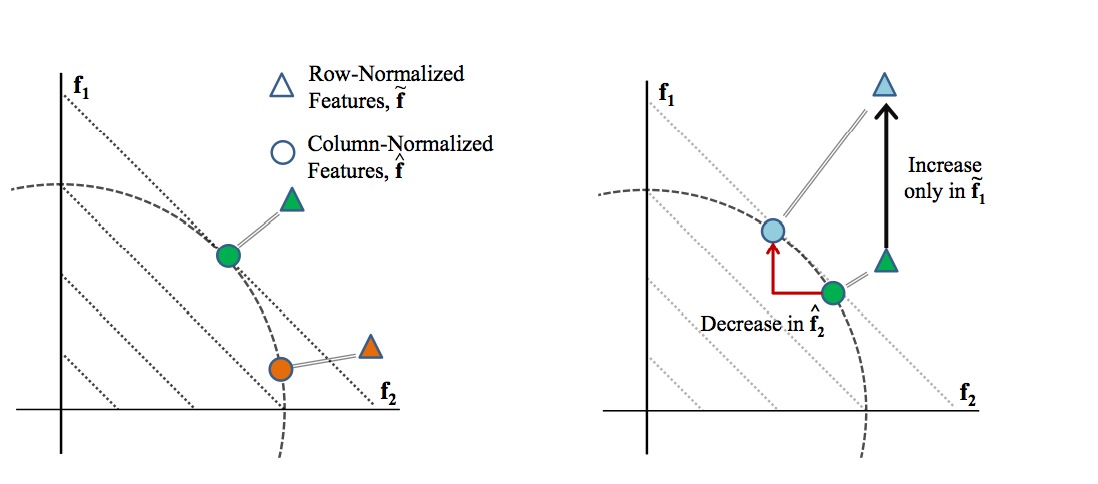
左图中, 假设只有两维特征, 并设定X,Y轴为这两维特征. 有绿色和红色两个样本, 三角代表俩样本正则化之前的坐标, 圆圈代表正则化之后的坐标. 正则化之后的样本的坐标都会落在虚线的圆上, 但是我们发现, 在这个圆上, 越接近坐标轴的点, 其$ell_1|)越小, 亦即如果我们以\(ell_1$为优化目标, 则样本的坐标会倾向于接近坐标轴, 亦即使得大部分特征值为0, 使得特征向量很稀疏. 右图说明了正则化会引入特征之间的竞争,亦即如果某一维特征的值($\tilde{\boldsymbol{f}_1}$)增加了, 则正则化后其他的特征值会降低($\tilde{\boldsymbol{f}_2}$).

2.2 对High Dispersal进行优化

在上述步骤中我们已经对每一个特征进行了正则化(第二步): $\hat{\boldsymbol{f}}^{(\boldsymbol{i})}={\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}/\|{\tilde{\boldsymbol{f}}}^{(\boldsymbol{i})}\|_2$, 亦即所有特征的期望激活平方为1,

2.3 对Lifetime Sparsity进行优化

如果我们已经限制了特征分布矩阵具有Population Sparsity和High Dispersal的特性, 则其也会拥Lifetime Sparsity的特性. 因为根据Population Sparsity, 特征分布矩阵中只会有很少的非零项, 而根据High Dispersal, 每个特征的分布都差不多, 所以每个特征应该都是比较稀疏的, 否则就违背了M是稀疏的这一条件.

参考文献:

[1]. Sparse Filtering. Jiquan Ngiam, Pang Wei Koh, Zhenghao Chen, Sonia Bhaskar, Andrew Y. Ng.