【贪心】【CF1061D】 TV Shows

Description

给定 \(n\) 个电视节目和两个参数 \(x,y\)。你想要看全部的电视节目，但是同一个电视机同一个时刻只能播放一个电视节目，所以你只能多租赁电视机。在时间 \([l,r]\) 租赁一台电视机的花费是 \(x~+~y~(r - l)\)。一台电视机不可以在节目没有播放完时中断播放。求最小花费。答案对 \(1e9+7\) 取模

Input

第一行是三个整数 \(n, x, y\)

下面 \(n\) 行每行两个整数 \(l,r\)，代表节目时间

Output

一行一个整数代表答案对 \(1e9+7\) 取模的结果

Hint

\(1~\leq~n~\leq~10^5~,~1~\leq~y~<~x~\leq~10^9~,~1~\leq~l~\leq~r~\leq~10^9\)

Solution

考虑贪心，有如下结论：

一、如果必须租赁新的电视机，在结束租赁的时间一定的情况下，租赁时间越晚越好。

这个结论显然，因为租赁时间越晚，租赁时长的代价越低。

二、如果前面有好几台空闲的电视机可以用，在不考虑租赁新的电视机时，一定选择上次结束时间最靠后的一台。

例如：

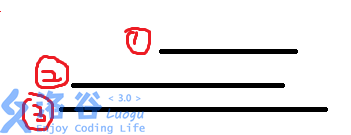
我们一定选择三号机器而不是一号二号，因为这样“浪费”的时间更少，即从上个节目结束到这个节目开始的时间花费更少。考虑如果后面紧跟着还有一个节目（开始时当前节目未结束），则它会选择一号，与这次选择一号下次选择三号相比，答案不会更劣。

以上是感性的理解结论二，下面给出结论二的证明（参考自官方题解）：

先将节目顺序按照左端点排序。因为每个节目时长再乘 \(y\) 是的花费是不变的，因此我们只比较额外的花费。即租赁新电视机的花费和续时的花费。下面的花费均值额外花费

考虑我们有两个用过的电视机 \(o1,o2\)，其中 \(r_{o1}~<~r_{o2}\)， \(r\) 为该电视上个节目的结束时间。当前我们要分配 \(i\) 这个节目。

下面分三种情况：

第一种：

如果后面不存在一个 \(j\) 使得从两个中继承过来比新租一个更划算的话，显然把 \(o2\) 分配给 \(i\) 更优

第二种：

如果后面存在一个 \(j\)，使得 \((l_j ~-~r_{o2})~y~\leq~x~~(1)\)，但是 \((l_j ~-~r_{o1})~y~>~x~~(2)\)，我们如果将 \(o1\) 分配给 \(i\)，那么花费是 \((l_j~-~r_{o2})~y~+~(l_i~-~r_{o1})~y~~(3)\)。考虑将 \(o2\) 分配给 \(i\)，那么花费是 \((r_l~-~r_{o1})~y~+~x~~(4)\)。给 \((2)\) 式左右同加 \((l_i~-~r_{o2})~y\) 即得 \((l_j ~-~r_{o1})~y~+~(l_i~-~r_{o2})~y>~x~+~(l_i~-~r_{o2})~y\)，即 \((3)~>~(4)\)，所以讲 \(o2\) 分配给 \(i\) 更优

第三种：

如果后面存在一个 \(j\)，使得 \((l_j ~-~r_{o2})~y~\leq~x~~(1)\)，并且 \((l_j ~-~r_{o1})~y~\leq~x~~(2)\)，那么这两种分配方式分别花费是 \((l_j~-~r_{o2})y~+~(l_i~-~r_{o1})y~=~y(l_j~+~l_i~-~r_{o2}~-~r_{o1})\) 和 \((l_i~-~r_{o2})y~+~(l_j~-~r_{o1})y~=~y(l_j~+~l_i~-~r_{o2}~-~r_{o1})\)。所以上两式是相等的，选择 \(o2\) 给 \(i\) 不会更劣。证毕。

那么我们就有如上两个贪心策略，每次比较贪心策略那个更优即可。即：新选择一个电视机租赁或者选择上次结束时间最靠后的一个电视机。根据结论一，如果选上次租赁过的而不是新租赁一个更好的话，因为新租赁电视机的时间被推迟了，答案一定不会更劣。于是这个贪心是正确的。

Code

#include <cstdio>
#include <algorithm>
#ifdef ONLINE_JUDGE
#define freopen(a, b, c)
#endif
#define rg register
#define ci const int
#define cl const long long

typedef long long int ll;

namespace IPT {
	const int L = 1000000;
	char buf[L], *front=buf, *end=buf;
	char GetChar() {
		if (front == end) {
			end = buf + fread(front = buf, 1, L, stdin);
			if (front == end) return -1;
		}
		return *(front++);
	}
}

template <typename T>
inline void qr(T &x) {
	rg char ch = IPT::GetChar(), lst = ' ';
	while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();
	while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();
	if (lst == '-') x = -x;
}

template <typename T>
inline void ReadDb(T &x) {
	rg char ch = IPT::GetChar(), lst = ' ';
	while ((ch > '9') || (ch < '0')) lst = ch, ch = IPT::GetChar();
	while ((ch >= '0') && (ch <= '9')) x = x * 10 + (ch ^ 48), ch = IPT::GetChar();
	if (ch == '.') {
		ch = IPT::GetChar();
		double base = 1;
		while ((ch >= '0') && (ch <= '9')) x += (ch ^ 48) * ((base *= 0.1)), ch = IPT::GetChar();
	}
	if (lst == '-') x = -x;
}

namespace OPT {
	char buf[120];
}

template <typename T>
inline void qw(T x, const char aft, const bool pt) {
	if (x < 0) {x = -x, putchar('-');}
	rg int top=0;
	do {OPT::buf[++top] = x % 10 + '0';} while (x /= 10);
	while (top) putchar(OPT::buf[top--]);
	if (pt) putchar(aft);
}

const int maxn = 100010;
const int maxm = 200010;
const int MOD = 1000000007;

struct M {
	int l, r;
	inline bool operator<(const M &_others) const {
		return this->r < _others.r;
	}
};
M MU[maxn];

struct Zay {
	int id, pos;
	bool Is_Begin;
	inline bool operator<(const Zay &_others) const {
		if (this->pos != _others.pos) return this->pos < _others.pos;
		else if (this->Is_Begin ^ _others.Is_Begin) return this->Is_Begin;
		else return this->id < _others.id;
	}
};
Zay CU[maxm];

int n, x, y, cnt, scnt, ans;
int stack[maxm];

int main() {
	freopen("1.in", "r", stdin);
	qr(n); qr(x); qr(y);
	for (rg int i = 1; i <= n; ++i) {
		qr(MU[i].l); qr(MU[i].r);
		Zay &_temp = CU[++cnt];
		_temp.id = i; _temp.pos = MU[i].l; _temp.Is_Begin = true;
		Zay &_tp = CU[++cnt];
		_tp.id = i; _tp.pos = MU[i].r;
	}
	std::sort(CU + 1, CU + 1 + cnt);
	for (rg int i = 1; i <= cnt; ++i) {
		if (CU[i].Is_Begin) {
			ll payd = x + 1ll * (MU[CU[i].id].r - MU[CU[i].id].l) * y;
			if (scnt) {
				if ((1ll * (MU[CU[i].id].r - stack[scnt]) * y) < payd) {
					payd = 1ll * (MU[CU[i].id].r - stack[scnt]) * y;
					--scnt;
				}
			}
			ans = (ans + payd) % MOD;
		} else {
			stack[++scnt] = CU[i].pos;
		}
	}
	qw(ans, '\n', true);
	return 0;
}