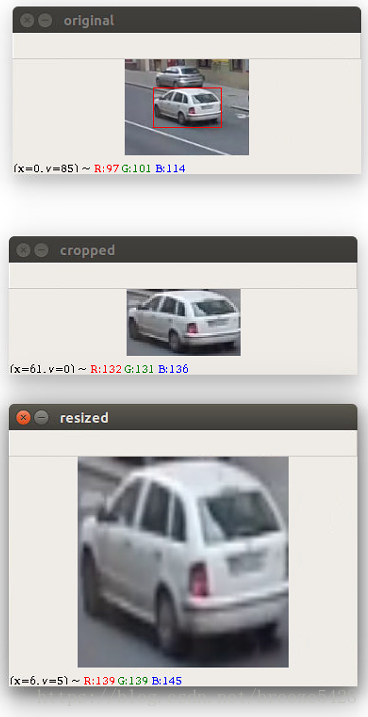
crop和resize操作区别

crop:对图像进行剪切

resize：对图像进行伸缩

实践代码

import cv2
bb2d = [30, 30, 72 ,42]
image = cv2.imread('car.png')
pt1 = (int(bb2d[0]), int(bb2d[1]))
pt2 = (int(bb2d[0]) + int(bb2d[2]), int(bb2d[1]) + int(bb2d[3]))
cv2.rectangle(image, pt1, pt2, (0,0,255))
cv2.imshow('original',image)
image = cv2.imread('car.png')
image_cropped = image[int(bb2d[1]):int(bb2d[1]) + int(bb2d[3]),
                      int(bb2d[0]):int(bb2d[0]) + int(bb2d[2])]
cv2.imshow('cropped',image_cropped)
image_resized = cv2.resize(image_cropped,(224,224))
cv2.imshow('resized',image_resized)
cv2.waitKey(0)

运行结果