P1183 多边形的面积

一道睡论数论题

其实是AC300祭才做的水题

题意：

很直白的的题意啊，就是求任意一个多边形的面积

所以我们来安利一下一个求多边形面积的数学通式：

给定多边形的顶点坐标（有序），让你来求这个多边形的面积，你会怎么做？

我们知道，任意多边形都可以分割为N个三角形，所以，如果以这为突破点，那么我们第一步就是把给定的多边形，分割为数个三角形，分别求面积，最后累加就可以了，把多边形分割为三角形的方式多种多样，在这里，我们按照如下图的方法分割：



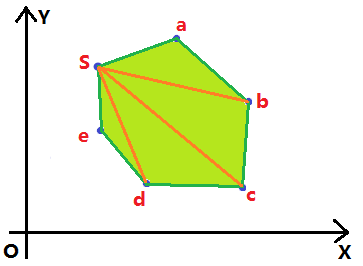
S点作为起始点（点1），a->e依次作为点2,3……。

一个三角形的面积是怎样的呢？

根据线性代数的知识，我们有如下的三角形面积公式，称之为有向面积：



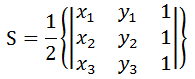
将这个行列式以第三列展开可以得到：



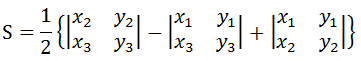
这就是以点1、2、3构成的三角形的有向面积（点如果是顺时针给出，有向面积为负，逆时针给出，有向面积为正），那么继续我们的工作，通过三角形的面积公式，来得到多边形的面积公式：

对于图1而言，多边形的面积就是：

S(1->6)=S(1,2,3)+S(1,3,4)+S(1,4,5)+S(1,5,6)

并且这样做对任意多边形都成立

所以，就有这样的公式：

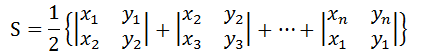
简化得：

$S_\Omega = \frac{1}{2} \sum_{k=1}^{\infty} (x_k y_{k + 1} - x_{k + 1} y_k) $

然后就能愉快的水掉这道题了。

CODE:

#include<iostream>
#include<cstdio>
#include<algorithm>
#define N 510 
using namespace std;
double x[N],y[N],ans;
int n;
int main() {
    scanf("%d",&n);
    for(int i = 1 ; i <= n ; i++)
    	scanf("%lf%lf",&x[i],&y[i]);
    x[0] = x[n];
    y[0] = y[n];
    for(int i = 0 ; i < n ; i++)
        ans += 0.5 * (x[i] * y[i + 1] - y[i] * x[i + 1]);
    printf("%d\n",int(ans) );
    return 0;
}