gitlab备份与还原

1、备份

　　登录原服务器，执行命令：

gitlab-rake gitlab:backup:create

　　备份后文件在如下目录，下载该文件

/var/opt/gitlab/backups

2.还原

　　先安装目标gitlab服务器，还原必须相同版本，版本号在此位置查找。安装指定版本的gitlab参见：https://www.cnblogs.com/rslai/p/9109624.html

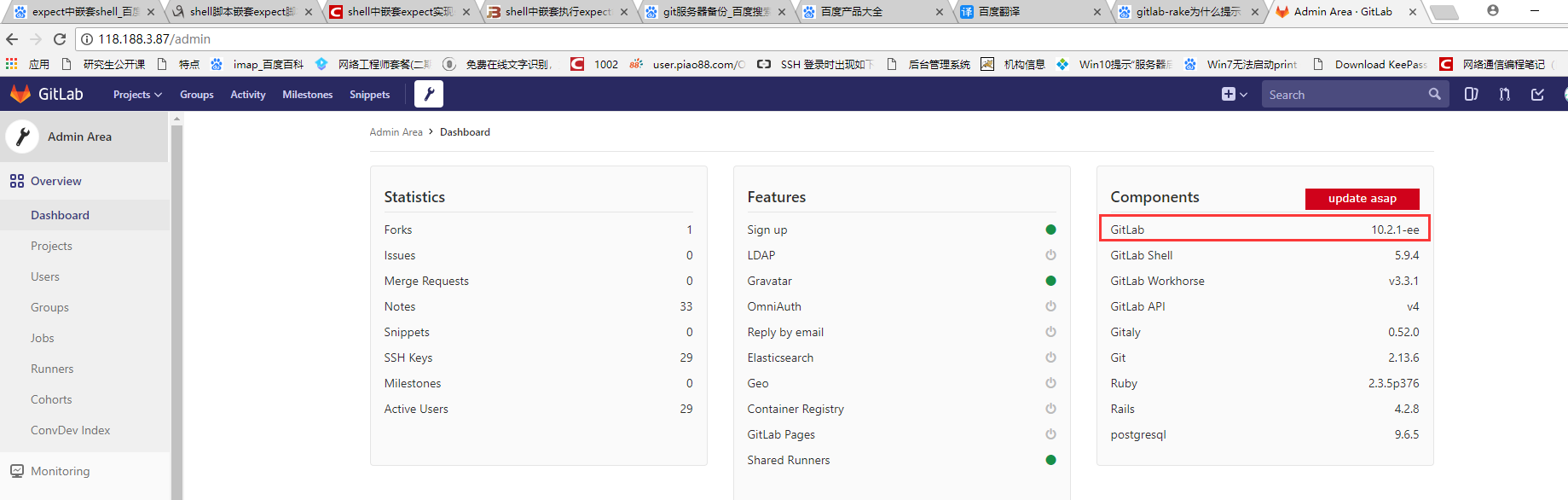
　　登录目标B服务器，将下载的备份文件上传到如下目录

/var/opt/gitlab/backups

　　还原备份文件，其中1527609906_2018_05_30_10.2.1-ee是你备份文件名的一部分

gitlab-rake gitlab:backup:restore RAILS_ENV=production BACKUP=1527609906_2018_05_30_10.2.1-ee

　　

参考文档：

　　http://www.xuliangwei.com/xubusi/803.html

　　https://www.cnblogs.com/kevingrace/p/7821529.html

　　https://blog.csdn.net/u010875635/article/details/70170169

　　https://blog.csdn.net/jenyzhang/article/details/53928438