【BZOJ 4558】 4558: [JLoi2016]方 （计数、容斥原理）

未经博主同意不能转载

4558: [JLoi2016]方

Time Limit: 20 Sec  Memory Limit: 256 MB
Submit: 362  Solved: 162

Description

上帝说，不要圆，要方，于是便有了这道题。由于我们应该方，而且最好能够尽量方，所以上帝派我们来找正方形

上帝把我们派到了一个有N行M列的方格图上，图上一共有(N+1)×(M+1)个格点，我们需要做的就是找出这些格点形

成了多少个正方形（换句话说，正方形的四个顶点都是格点）。但是这个问题对于我们来说太难了，因为点数太多

了，所以上帝删掉了这(N+1)×(M+1)中的K个点。既然点变少了，问题也就变简单了，那么这个时候这些格点组成

了多少个正方形呢？

Input

第一行三个整数 N, M, K， 代表棋盘的行数、 列数和不能选取的顶点个数。 保证 N, M >= 1， K <=(N + 1) ×

(M + 1)。约定每行的格点从上到下依次用整数 0 到 N 编号，每列的格点依次用 0到 M 编号。接下来 K 行，每

行两个整数 x,y 代表第 x 行第 y 列的格点被删掉了。保证 0 <=x <=N<=10^6, 0 <=y<=M<=10^6，K<=2*1000且不

会出现重复的格点。

Output

仅一行一个正整数， 代表正方形个数对 100000007（ 10^8 + 7） 取模之后的值

Sample Input

2 2 4
1 0
1 2
0 1
2 1

Sample Output

1

HINT

Source

【分析】

　　终于A了，昨晚做了一晚上了。

　　容斥真的很容易搞错。

　　注意这题的正方形可以是【斜着的】

　　于是怎么算呢？首先假设没有删除点，答案=总方案-至少有一个删除点的方案数

　　1、总方案怎么算？

　　你会觉得斜着的正方形很难算，但是每个正方形都有外接正方形，对于边长为a的正的正方形来说，他是a个正方形的外接正方形，于是枚举外接正方形边长即可。

　　2、至少有一个删除点的方案数？

　　这个的答案=SIGEMA（枚举每一个删除点然后算以他为顶点的正方形的方案数）-至少两个删除点的方案数+至少三个删除点的方案数-4个删除点的方案数

　　3、枚举每一个删除点然后算以他为顶点的正方形的方案数？

　　【这里的正方形还是有斜的】，但是！这个删除点一定在这个以它的顶点的正方形的外接正方形的某条边长上（或角上），所以只需计算正的正方形且某条边长覆盖这个点的方案数。

　　【这个貌似是最难算的，因为看不懂题解于是我自己Y了一个计算方法】：

　　

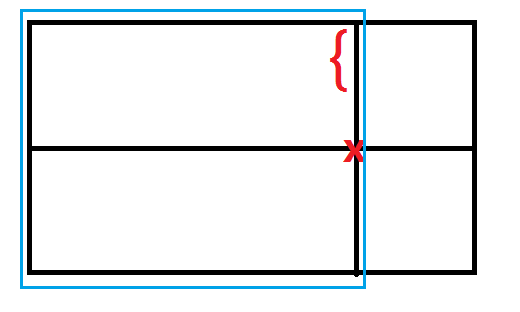
　　分成四部分来做（还有一部分是删除点是顶点，这个比较容易就不说了，所以现在计算的答案是不包含删除点是顶点的，只包含删除点在四边上）

　　四部分是左半、右半、上半、下半，图示蓝框是左半。

　　左半部分就是说删除点在正方形右边长上。

　　【还是把正方形画一画吧】

　　

　　　根据蓝框的横宽可以知道正方形边长的一个极限，于是可以把图形降维，变成一维上的问题。

　　

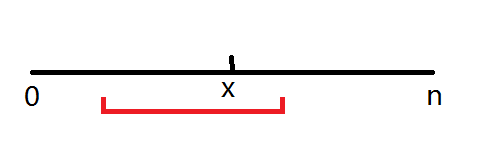
　　问题变成：0~n数轴上有一点x，问你长度为[1,r]且为整数的，并覆盖了x点的区间有多少个（端点覆盖不算覆盖）。

　　之前做的一道概率题已让我对此问题有所体会，这里再用一个小容斥最好算了：总区间-不覆盖x的区间。

　　即(0~n)中长度[1,r]的整区间-(0~x)中长度[1,r]的整区间-(x~n)中长度[1,r]的整区间。

　　这样就求出来了这个答案，记为a1。【记得要把删除点为正方形角的加上

　　4、问题还没有结束，对于2个、3个、4个删除点，我们枚举两个删除点可以确定这个正方形（有三种形态）

　　然后这三个答案一起算。记为a2，a3，a4

　　最后答案=总-a1+a2-a3/3+a4/6【因为你枚举两个点，所以同一个正方形有可能算多遍，于是需要除,a3加的时候是加TMP，具体看代码】

　　【说一下这个为什么？我其实我己都没想清楚这个，也是看别人这样写的】

　　首先a2计算是正确的，你假设两个未删除点，枚举的也是两个未删除点。

　　a3的话，你应该枚举三个未删除的点，但是你只枚举两个，第三个是计算出来的。

　　假设真的只有三个点，对于同一个正方形，你枚举了$C_{3}^{2}$次，实际上应该枚举$C_{3}^{3}$次，是3倍，所以要除以3。

　　不过至少是3的话还有可能是4，你枚举了$C_{4}^{2}$次，实际上应该枚举$C_{4}^{3}$次，所以要*2/3

　　a4的话，你枚举了$C_{4}^{2}$次，实际是$C_{4}^{4}$次，所以要除以6。

　　确定正方形的三种形态的话，我也是自己Y了一下，经验就是用向量！，向量是解决几何问题的最好工具！【不懂可以看看代码怎么打

　　

　　【这篇写得够认真了吧？？】

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 2010
 #define Maxm 1000010
 #define Mod 100000007
 #define LL long long

 int mymin(int x,int y) {return x<y?x:y;}

 int nx[Maxn],ny[Maxn],rx[Maxm],ry[Maxm];
 bool vis[Maxn][Maxn];

 struct node
 {
     int x,id;
 }t[Maxn];
 bool cmp(node x,node y) {return x.x<y.x;}

 int check(int x,int y)
 {
     int ret=;
     if(vis[nx[x]][ny[x]]) ret++;
     if(vis[nx[y]][ny[y]]) ret++;
     if(vis[nx[x]][ny[y]]) ret++;
     if(vis[nx[y]][ny[x]]) ret++;
     return ret;
 }

 int n,m,k;
 void init()
 {
     for(int i=;i<=k;i++) t[i].x=nx[i],t[i].id=i;sort(t+,t++k,cmp);
     int p=;rx[t[].x]=p;
     for(int i=;i<=k;i++)
     {
         if(t[i].x!=t[i-].x) p++,rx[t[i].x]=p;
         // nx[t[i].id]=p;
     }
     for(int i=;i<=k;i++) t[i].x=ny[i],t[i].id=i;sort(t+,t++k,cmp);
     p=;ry[t[].x]=p;
     for(int i=;i<=k;i++)
     {
         if(t[i].x!=t[i-].x) p++,ry[t[i].x]=p;
         // ny[t[i].id]=p;
     }
     memset(vis,,sizeof(vis));
     for(int i=;i<=k;i++) vis[rx[nx[i]]][ry[ny[i]]]=;
 }

 int cal(int x,int y)
 {
     if(!x) return ;
     y=min(y,x);
     int l=x-y+,r=x;
     return (1LL*(l+r)*(r-l+)/)%Mod;
 }

 int a1,a2,a3,a4;
 void get_ans(int x1,int y1,int x2,int y2)
 {
     if(x1<||x1>n||y1<||y1>m||x2<||x2>n||y2<||y2>m) return;
     int tmp=;
     if(rx[x1]&&ry[y1]&&vis[rx[x1]][ry[y1]]) tmp++;
     if(rx[x2]&&ry[y2]&&vis[rx[x2]][ry[y2]]) tmp++;
     a2++;if(tmp) a3+=tmp;if(tmp>) a4++;
 }

 void solve(int x1,int y1,int x2,int y2)
 {
     int dx=x1-x2,dy=y1-y2;
     get_ans(x1+dy,y1-dx,x2+dy,y2-dx);
     get_ans(x1-dy,y1+dx,x2-dy,y2+dx);
     if(abs(dx+dy)&) return;
     get_ans((x1+x2+dy)/,(y1+y2-dx)/,(x1+x2-dy)/,(y1+y2+dx)/);
 }

 int main()
 {
     scanf("%d%d%d",&n,&m,&k);
     int ans=;
     for(int i=;i<=n&&i<=m;i++) ans=(ans+1LL*(n+-i)*(m+-i)%Mod*i%Mod)%Mod;
     for(int i=;i<=k;i++)
     {
         scanf("%d%d",&nx[i],&ny[i]);
     }
     for(int i=;i<=k;i++)
     {
         a1+=cal(n,ny[i])-cal(nx[i],ny[i])-cal(n-nx[i],ny[i]);a1%=Mod;
         a1+=cal(n,m-ny[i])-cal(nx[i],m-ny[i])-cal(n-nx[i],m-ny[i]);a1%=Mod;
         a1+=cal(m,nx[i])-cal(ny[i],nx[i])-cal(m-ny[i],nx[i]);a1%=Mod;
         a1+=cal(m,n-nx[i])-cal(ny[i],n-nx[i])-cal(m-ny[i],n-nx[i]);a1%=Mod;
         a1+=min(nx[i],ny[i])+min(n-nx[i],m-ny[i])+min(n-nx[i],ny[i])+min(nx[i],m-ny[i]);a1%=Mod;
     }
     init();
     for(int i=;i<=k;i++)
      for(int j=i+;j<=k;j++)
      {
         solve(nx[i],ny[i],nx[j],ny[j]);
      }
     // printf("%d\n",a3);
     printf("%d\n",((ans-a1+a2-a3/+a4/)%Mod+Mod)%Mod);
     return ;
 }

2017-04-21 09:25:43