[xsy2213]tower

题意：给一个地图，地图上的每个位置是空地或一个炮或一些敌人，给定每个炮的方向（上/下/左/右），每个炮只能打一个位置且炮弹轨迹不能相交，问最多打到多少敌人

原题貌似是TC SRM 627的题，题解在这里

考虑一开始让每个炮都打敌人最多的位置，这样轨迹有可能相交，我们要做的就是合理规划，缩短某些炮击的距离使轨迹不相交的同时能打到的敌人减少量最少

对于水平炮，我们这样建图：

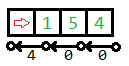
即：假设$y$是$x$往炮方向的第一个点，如果$x$的敌人数量比炮能打到的最多敌人数量少$v$，那么连边$(x,y,v)$

对于竖直炮，我们这样建图：

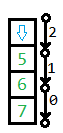
即：假设$x$是$y$往炮方向的第一个点，如果$y$的敌人数量比炮能打到的最多敌人数量少$v$，那么连边$(x,y,v)$

对于这个图的竖边，如果我们割掉$(x,y,v)$，那么就相当于让某个竖直炮打$y$，并且它比最优情况打少了$v$个敌人，横边类似

如果我们把竖直炮设为源点，水平炮设为汇点，那么因为不能相交，所以我们割掉一些边（决定了某些炮的打击目标）后，不能有任何一条从源点到汇点的路径，所以就相当于求最小割

这样还会有一个问题：我们要割掉先走竖边再走横边（炮弹轨迹不能相交），但是交错走横竖边是被允许的，所以我们还要从（竖边连接的点）向对应的（横边连接的点）连一条$+\infty$的边，确保先走竖再走横的路径会被割掉

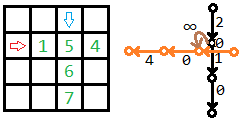
所以最后的答案就是每个炮能打到的最多敌人数量加起来再减去最小割

#include<stdio.h>
#include<string.h>
const int inf=2147483647;
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
int h[5010],cur[5010],nex[30010],to[30010],cap[30010],q[30010],dis[5010],M=1,S,T;
void add(int a,int b,int c){
	M++;
	to[M]=b;
	cap[M]=c;
	nex[M]=h[a];
	h[a]=M;
	M++;
	to[M]=a;
	cap[M]=0;
	nex[M]=h[b];
	h[b]=M;
}
bool bfs(){
	int x,i,head,tail;
	head=tail=1;
	q[1]=S;
	memset(dis,-1,sizeof(dis));
	dis[S]=0;
	while(head<=tail){
		x=q[head];
		head++;
		for(i=h[x];i;i=nex[i]){
			if(cap[i]&&dis[to[i]]==-1){
				dis[to[i]]=dis[x]+1;
				if(to[i]==T)return 1;
				tail++;
				q[tail]=to[i];
			}
		}
	}
	return 0;
}
int dfs(int x,int flow){
	if(x==T)return flow;
	int i,f;
	for(i=cur[x];i;i=nex[i]){
		if(cap[i]&&dis[to[i]]==dis[x]+1){
			f=dfs(to[i],min(flow,cap[i]));
			if(f){
				cap[i]-=f;
				cap[i^1]+=f;
				if(cap[i])cur[x]=i;
				return f;
			}
		}
	}
	dis[x]=-1;
	return 0;
}
int dicnic(){
	int ans=0,tmp;
	while(bfs()){
		memcpy(cur,h,sizeof(h));
		while(tmp=dfs(S,100000000))ans+=tmp;
	}
	return ans;
}
int n,m,s[60][60],tmp[60];
const int go[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
bool ok(int x,int y){return 0<x&&x<=n&&0<y&&y<=m;}
int ve(int x,int y){return(x-1)*m+y;}
int ho(int x,int y){return(x-1)*m+y+n*m;}
void move(int&x,int&y,int f){
	x+=go[f][0];
	y+=go[f][1];
}
int main(){
	int i,j,x,y,f,cnt,sum,mx;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++)scanf("%d",s[i]+j);
	}
	S=n*m*2+1;
	T=n*m*2+2;
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++)add(ve(i,j),ho(i,j),inf);
	}
	sum=0;
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			if(s[i][j]<0){
				x=i;
				y=j;
				f=-s[i][j]-1;
				cnt=0;
				while(ok(x,y)){
					cnt++;
					tmp[cnt]=max(tmp[cnt-1],s[x][y]);
					move(x,y,f);
				}
				mx=tmp[cnt];
				sum+=mx;
				move(x,y,f^1);
				while(x!=i||y!=j){
					cnt--;
					if(f<2)
						add(ve(x-go[f][0],y-go[f][1]),ve(x,y),mx-tmp[cnt]);
					else
						add(ho(x,y),ho(x-go[f][0],y-go[f][1]),mx-tmp[cnt]);
					move(x,y,f^1);
				}
				if(f<2)
					add(S,ve(i,j),inf);
				else
					add(ho(i,j),T,inf);
			}
		}
	}
	printf("%d",sum-dicnic());
}