《机器学习实战》学习笔记第十一章 —— Apriori算法

主要内容：

一.关联分析

二.Apriori原理

三.使用Apriori算法生成频繁项集

四.从频繁项集中生成关联规则

一.关联分析

1.关联分析是一种在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式：频繁项集和关联规则。

2.频繁项集是经常出现在一起的元素的集合。

3.关联规则暗示两个元素集合之间可能存在很强的关系。形式为：A——>B，就是“如果A，则B”。

4.支持度：数据集中包含该项集的数据所占的比例，支持度高的项集就为频繁项集。

5.可信度（置信度）：衡量关联规则可信程度的标准，假设A出现的概率为P（A），AB出现的概率为P（AB），则可信度为P（B|A） = P（AB）/ P（A）。

二.Apriori原理

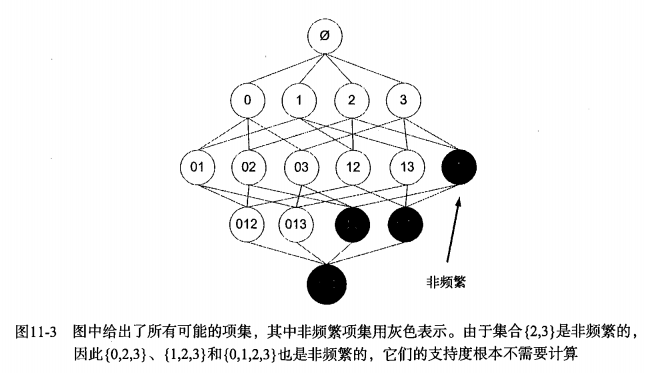
1.Apriori原理是说如果某个项集是频繁的，那么它的所有子集也是频繁的。p --> q  ==>   !q --> !p ，所以：如果一个项集是非频繁项集，那么它的所有超集也是非频繁项集。

2.Apriori原理可以帮我们去除掉很多非频繁项集。因为我们可以在项集规模还是很小的时候，假如能确定他是非频繁的，那么就可以直接去除掉那些含有该项集的更大的项集了，从而减少了运算的规模。

3.例子如下：

三.使用Apriori算法生成频繁项集

1.算法步骤：

1）根据数据集，生成单位项集C1，然后计算项集C1的支持度，并从中挑选出频繁项集构成L1（频繁项集的划分边界为一个阈值 Mini support）。

2）设已经完成的最新一层的频繁项集的项数为k，而这一层可称为第k层，可知k初始化为1。判断这一层频繁项集的个数是否大于1：如果大于1，则表明至少存在两个频繁项集可以两两合并成一个新的项集Ck+1，然后计算其支持度并过滤出频繁项集，生成第k+1层。

3）重复执行第2）步，直到最新一层的频繁项集的个数少于等于1。

注：两个频繁项集合并时，需要限定：两者有k-1个元素是相同的，然后两者合并之后，就形成了一个k+1的集合。假如两个频繁项集的相同元素少于k-1个，那他们合并后的新项集的项数必定大于k+1，对于此种情况就直接忽略掉，让它在往后的那些层再重新被考虑。这样就能够保证每一层的频繁项集的项数是相同的。

2算法流程图：

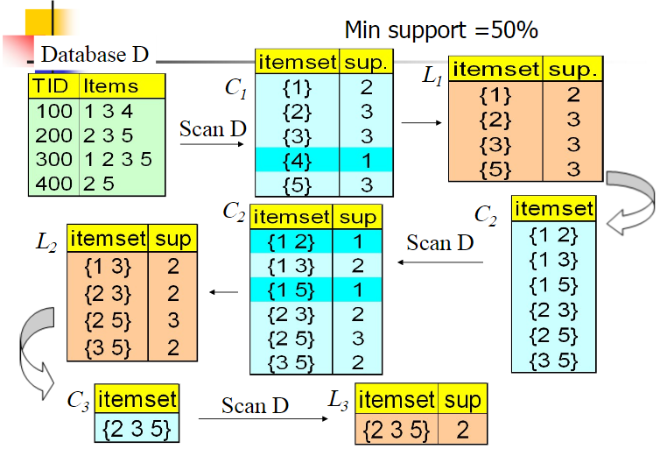
3.Python代码：

 def createC1(dataSet):      #生成单位项集
     C1 = []
     for transaction in dataSet:     #枚举每一条数据
         for item in transaction:        #枚举每条数据中的每个元素
             if not [item] in C1:
                 C1.append([item])       #将素有元素加入列表中
     C1.sort()           #必要的排序
     return map(frozenset, C1)  # use frozen set so we  can use it as a key in a dict

 def scanD(D, Ck, minSupport):   #计算项集的支持度，并过滤掉支持度低于阈值的项集，从而形成频繁项集。Ck的k代表项集的项数
     ssCnt = {}
     for tid in D:   #统计项集在数据中的出现次数
         for can in Ck:
             if can.issubset(tid):
                 if not ssCnt.has_key(can):
                     ssCnt[can] = 1
                 else:
                     ssCnt[can] += 1
     numItems = float(len(D))
     retList = []    #频繁项集列表
     supportData = {}    #保存项集的支持度，是一个字典。注意：非频繁项集也保存。
     for key in ssCnt:
         support = ssCnt[key] / numItems #支持度
         if support >= minSupport:
             retList.insert(0, key)  #频繁项集
         supportData[key] = support  #保存支持度
     return retList, supportData

 def aprioriGen(Lk, k):  # 用于生成下一层的频繁项集（即项数是当前一次的项数+1狼，即k）
     retList = []
     lenLk = len(Lk)
     for i in range(lenLk):  #O(n^2)组合生成新项集
         for j in range(i + 1, lenLk):
             L1 = list(Lk[i])[:k - 2]; L2 = list(Lk[j])[:k - 2]  #去除两者的前k-2个项
             L1.sort(); L2.sort()
             if L1 == L2:  # 如果前k-2个项相等，那么将Lk[i]和Lk[j]并在一起，就形成了k+1个项的项集
                 retList.append(Lk[i] | Lk[j])  # set union
     return retList

 def apriori(dataSet, minSupport=0.5):   #Apriori算法
     D = map(set, dataSet)   #set形式数据集（即去除重复的数据）
     C1 = createC1(dataSet)  #单位项集
     L1, supportData = scanD(D, C1, minSupport)  #单位频繁项集
     L = [L1]
     k = 2
     while (len(L[k - 2]) > 1):  #如果当层的频繁项集的个数大于1，那么就可以根据当层的频繁项集生成下一层的频繁项集
         Ck = aprioriGen(L[k - 2], k)    #生成下一层的项集
         Lk, supK = scanD(D, Ck, minSupport)  # 生成下一层的频繁项集，同时得到项集的支持度
         supportData.update(supK)    #更新支持度库
         L.append(Lk)    #把下一层的频繁项集加入到“层叠”里面
         k += 1  #将下一层作为当层
     return L, supportData

四.从频繁项集中生成关联规则

1.为何要从频繁项集中生成关联规则？因为频繁项集意味着出现的频率更高，从中得到的规则更能让人信服（这里不是指可信度）。举个反例，如果A和B只出现过一次，且两者一起出现即AB，我们就可以得到结论A-->B的可信度为100%，但AB的出现可能就是一个噪音，贸贸然下定论并非合理。所以要从频繁项集中生成关联规则。

2.如何从频繁项集中生成关联规则？简而言之就是挑选一个频繁项集，如{ABCD}，首先把它作为规则的前件，然后逐渐把元素往后件移，如A-->BCD、B-->ACD、C-->ABD、D-->ABC、AB-->CD……等等。但具体又如何操作呢？难道要用数学中组合的方式？这样计算量太大了。这里有个事实：如果某条规则并不满足最小可信度要求，那么该规则的所有子集也不会满足最小可信度要求。如下：

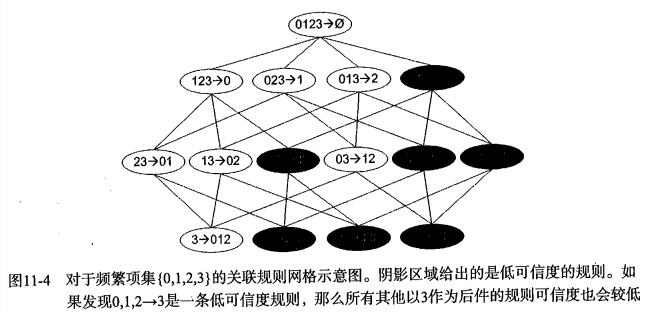
可知{0,1,2}-->{3}的可信度为 P（{3}）/ P（{0,1,2}），如果{0,1,2}-->{3}是低可信度规则，那么{0,1}-->{2,3} 、{2}-->{0,1,3}等等3在后件的那些规则，统统都为低可信度规则。原因就在于可信度的计算公式：对于{0,1,2}-->{3}，其可信度为P（{3}）/ P（{0,1,2}），此时如果把0从前件移到后件，那么就成了{1,2}-->{0,3}，其可信度为P（{0,3}）/ P（{1,2}），较之于P（{3}）/ P（{0,1,2}），其分子减小了，其分母增大了，所以P（{0,3}）/ P（{1,2}）< P（{3}）/ P（{0,1,2}）。所以：如果{0,1,2}-->{3}是低可信度规则，那么{1,2}-->{0,3}也是低可信度规则。

简而言之：对于在同一个频繁项集内形成的关联规则，假如某规则为低可信度规则，那么规则后件是该低可信度规则后件的超集的规则，都是低可信度规则。因此可以直接去掉。

3.算法流程：

1）枚举每一层的每一个频繁项集，将其作为生成关联规则的当前项集freSet，同时将freSet的单个元素作为单位项集以作为关联规则后件H。

2）如果关联规则后件的项数小于当前项集freSet的项数，则前件后件都不为空，此时：枚举关联后件H，将freSet-H作为前件，将H作为后件，然后计算其可信度，并筛选出可信度高的关联规则，同时筛选出能生成高可信度规则的后件H（大大简化计算量）。

3）如果筛选过后的后件H的个数大于1，则表明可以生成当前后件项数+1的后件，那么就调用Apriori算法生成新一层的后件Hnext，将Hnext作为H，然后重复第2）步。

4.Python代码：

 def calcConf(freqSet, H, supportData, brl, minConf=0.7):    #计算关联规则的可信度，关联规则的右端的元素个数是固定的
     prunedH = []  # create new list to return
     for conseq in H:    #conseq作为关联规则的右端
         conf = supportData[freqSet] / supportData[freqSet - conseq]  # 计算可信度
         if conf >= minConf:     #可信度大于等于阈值，则将关联规则存储起来
             print freqSet - conseq, '-->', conseq, 'conf:', conf
             brl.append((freqSet - conseq, conseq, conf))        #将关联规则存储起来
             prunedH.append(conseq)  #将能生成关联规则的频繁项集存起来
     return prunedH

 def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
     m = len(H[0])      #关联规则的右端的元素个数
     if (len(freqSet) > m):  #如果总的元素个数大于关联规则的右端的元素个数，则继续生成关联规则
         Hitem = calcConf(freqSet, H, supportData, brl, minConf)     #生成关联规则， 同时过滤出有用的频发项集
         if (len(Hitem) > 1):  # 频繁项集的个数超过一个，则可以生成下一层的项集（即关联规则的元素个数右端加一，对应地左端减一）
             Hnext = aprioriGen(Hitem, m + 1)  # create Hm+1 new candidates
             rulesFromConseq(freqSet, Hnext, supportData, brl, minConf)

 def generateRules(L, supportData, minConf=0.7):  # 生成关联规则
     bigRuleList = []    #关联规则列表
     for i in range(1, len(L)):  # 枚举每一层（也可以说枚举长度，从第二层开始，因为关联最少要有两个元素）
         for freqSet in L[i]:    #枚举这一层中所有的频繁项集，用于生成关联规则
             H1 = [frozenset([item]) for item in freqSet]        #将频繁项集中的元素单独作为一个集合，然后这些集合构成一个列表
             rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf) #递归地将freqSet中的元素移到关联规则的右端，从而生成关联规则
     return bigRuleList