POJ 2029 Get Many Persimmon Trees （二维树状数组）

Get Many Persimmon Trees

Time Limit:1000MS    Memory Limit:30000KB    64bit IO Format:%I64d
& %I64u

SubmitStatusPracticePOJ
2029

Description

Seiji Hayashi had been a professor of the Nisshinkan Samurai School in the domain of Aizu for a long time in the 18th century. In order to reward him for his meritorious career in education, Katanobu Matsudaira, the lord of the
domain of Aizu, had decided to grant him a rectangular estate within a large field in the Aizu Basin. Although the size (width and height) of the estate was strictly specified by the lord, he was allowed to choose any location for the estate in the field.
Inside the field which had also a rectangular shape, many Japanese persimmon trees, whose fruit was one of the famous products of the Aizu region known as 'Mishirazu Persimmon', were planted. Since persimmon was Hayashi's favorite fruit, he wanted to have
as many persimmon trees as possible in the estate given by the lord.

For example, in Figure 1, the entire field is a rectangular grid whose width and height are 10 and 8 respectively. Each asterisk (*) represents a place of a persimmon tree. If the specified width and height of the estate are 4 and 3 respectively, the area surrounded
by the solid line contains the most persimmon trees. Similarly, if the estate's width is 6 and its height is 4, the area surrounded by the dashed line has the most, and if the estate's width and height are 3 and 4 respectively, the area surrounded by the dotted
line contains the most persimmon trees. Note that the width and height cannot be swapped; the sizes 4 by 3 and 3 by 4 are different, as shown in Figure 1.



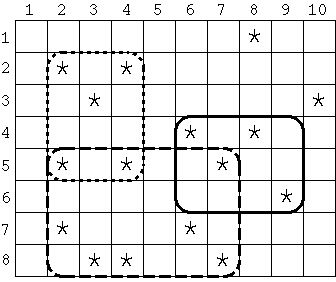
Figure 1: Examples of Rectangular Estates


Your task is to find the estate of a given size (width and height) that contains the largest number of persimmon trees.

Input

The input consists of multiple data sets. Each data set is given in the following format.



N

W H

x1 y1

x2 y2

...

xN yN

S T



N is the number of persimmon trees, which is a positive integer less than 500. W and H are the width and the height of the entire field respectively. You can assume that both W and H are positive integers whose values are less than 100. For each i (1 <= i <=
N), xi and yi are coordinates of the i-th persimmon tree in the grid. Note that the origin of each coordinate is 1. You can assume that 1 <= xi <= W and 1 <= yi <= H, and no two trees have the same positions. But you should not assume that the persimmon trees
are sorted in some order according to their positions. Lastly, S and T are positive integers of the width and height respectively of the estate given by the lord. You can also assume that 1 <= S <= W and 1 <= T <= H.



The end of the input is indicated by a line that solely contains a zero.

Output

For each data set, you are requested to print one line containing the maximum possible number of persimmon trees that can be included in an estate of the given size.

Sample Input

16
10 8
2 2
2 5
2 7
3 3
3 8
4 2
4 5
4 8
6 4
6 7
7 5
7 8
8 1
8 4
9 6
10 3
4 3
8
6 4
1 2
2 1
2 4
3 4
4 2
5 3
6 1
6 2
3 2
0

Sample Output

4
3

大致题意：国王所在的领地有W*H个点，当中n个点处有树， 如今领地上最多同意圈（当然能够少于）大小为S*T的矩形，问最多可圈中多少棵树？

解题思路：枚举起点，用二维树状数组求解。

枚举起点时要注意从行列从S和T開始。直到W和H为止。

用二维树状数组时。要注意update（）每次更新时，c[ ] 加的是1。

AC代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int maxn = 102;
int n, w, h, s, t;
int c[maxn][maxn];

int lowbit(int x){ return x&(-x); }

void update(int x,int y){
	for(int i=x; i<maxn; i+=lowbit(i))
		for(int j=y; j<maxn; j+=lowbit(j))
			c[i][j] ++;
}

long long sum(int x, int y){
	long long ans = 0;
	for(int i=x; i>0; i-=lowbit(i))
		for(int j=y; j>0; j-=lowbit(j))
			ans += c[i][j];
	return ans;
}

int main(){
	#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	#endif
	int x, y;
	while(~scanf("%d", &n) && n){
		scanf("%d%d", &w, &h);
		memset(c,0,sizeof(c));
		for(int i=1; i<=n; i++){
			scanf("%d%d", &x, &y);
			update(x, y);
		}
		scanf("%d%d", &s, &t);
		long long ans = 0;
		for(int i=s; i<=w; i++)      //枚举起点
			for(int j=t; j<=h; j++)
				ans = max(ans, sum(i, j) - sum(i-s, j) - sum(i, j-t) + sum(i-s, j-t));    //树状数组求区域和
		printf("%lld\n", ans);
	}
	return 0;
}