基于OpenMP的矩阵乘法实现及效率提升分析

一．  矩阵乘法串行实现

例子选择两个1024*1024的矩阵相乘，根据矩阵乘法运算得到运算结果。其中，两个矩阵中的数为double类型，初值由随机数函数产生。代码如下：

#include <iostream>
#include <omp.h> // OpenMP编程需要包含的头文件
#include <time.h>
#include <stdlib.h>

using namespace std;

#define MatrixOrder 1024
#define FactorIntToDouble 1.1; //使用rand（）函数产生int型随机数，将其乘以因子转化为double型；

double firstParaMatrix [MatrixOrder] [MatrixOrder] = {0.0};
double secondParaMatrix [MatrixOrder] [MatrixOrder] = {0.0};
double matrixMultiResult [MatrixOrder] [MatrixOrder] = {0.0};

//计算matrixMultiResult[row][col]
double calcuPartOfMatrixMulti(int row,int col)
{
    double resultValue = ;
    for(int transNumber =  ; transNumber < MatrixOrder ; transNumber++) {
        resultValue += firstParaMatrix [row] [transNumber] * secondParaMatrix [transNumber] [col] ;
    }
    return resultValue;
}

/* * * * * * * * * * * * * * * * * * * * * * * * *
* 使用随机数为乘数矩阵和被乘数矩阵赋double型初值 *
* * * * * * * * * * * * * * * * * * * * * * * * */
void matrixInit()
{
    for(int row =  ; row < MatrixOrder ; row++ ) {
        for(int col =  ; col < MatrixOrder ;col++){
            srand(row+col);
            firstParaMatrix [row] [col] = ( rand() %  ) * FactorIntToDouble;
            secondParaMatrix [row] [col] = ( rand() %  ) * FactorIntToDouble;
        }
    }
}

/* * * * * * * * * * * * * * * * * * * * * * *
* 实现矩阵相乘 *
* * * * * * * * * * * * * * * * * * * * * * * */
void matrixMulti()
{
    for(int row =  ; row < MatrixOrder ; row++){
        for(int col = ; col < MatrixOrder ; col++){
            matrixMultiResult [row] [col] = calcuPartOfMatrixMulti (row,col);
        }
    }
}

int main()
{
    matrixInit();

    clock_t t1 = clock(); //开始计时；
    matrixMulti();
    clock_t t2 = clock(); //结束计时
      cout<<"time: "<<t2-t1<<endl; 

    system("pause");

    return ;
}  

二  矩阵乘法并行实现

使用#pragma omp parallel for为for循环添加并行，使用num_threads()函数指定并行线程数。

使用VS2010编译，需要先在项目属性中选择支持openmp，在头文件中包含<omp.h>即可使用openmp为矩阵乘法实现并行。

代码如下：

#include <iostream>
#include <omp.h> // OpenMP编程需要包含的头文件
#include <time.h>
#include <stdlib.h>

using namespace std;

#define MatrixOrder 1024
#define FactorIntToDouble 1.1; //使用rand（）函数产生int型随机数，将其乘以因子转化为double型；

double firstParaMatrix [MatrixOrder] [MatrixOrder] = {0.0};
double secondParaMatrix [MatrixOrder] [MatrixOrder] = {0.0};
double matrixMultiResult [MatrixOrder] [MatrixOrder] = {0.0};

//计算matrixMultiResult[row][col]
double calcuPartOfMatrixMulti(int row,int col)
{
    double resultValue = ;
    for(int transNumber =  ; transNumber < MatrixOrder ; transNumber++) {
        resultValue += firstParaMatrix [row] [transNumber] * secondParaMatrix [transNumber] [col] ;
    }
    return resultValue;
}

/* * * * * * * * * * * * * * * * * * * * * * * * *
* 使用随机数为乘数矩阵和被乘数矩阵赋double型初值 *
* * * * * * * * * * * * * * * * * * * * * * * * */
void matrixInit()
{
    #pragma omp parallel for num_threads(64)
    for(int row =  ; row < MatrixOrder ; row++ ) {
        for(int col =  ; col < MatrixOrder ;col++){
            srand(row+col);
            firstParaMatrix [row] [col] = ( rand() %  ) * FactorIntToDouble;
            secondParaMatrix [row] [col] = ( rand() %  ) * FactorIntToDouble;
        }
    }
    //#pragma omp barrier
}

/* * * * * * * * * * * * * * * * * * * * * * *
* 实现矩阵相乘 *
* * * * * * * * * * * * * * * * * * * * * * * */
void matrixMulti()
{

    #pragma omp parallel for num_threads(64)
    for(int row =  ; row < MatrixOrder ; row++){
        for(int col = ; col < MatrixOrder ; col++){
            matrixMultiResult [row] [col] = calcuPartOfMatrixMulti (row,col);
        }
    }
    //#pragma omp barrier
}

int main()
{
    matrixInit();

    clock_t t1 = clock(); //开始计时；
    matrixMulti();
    clock_t t2 = clock(); //结束计时
      cout<<"time: "<<t2-t1<<endl; 

    system("pause");

    return ;
}  

三 效率对比

运行以上两种方法，对比程序运行时间。

当矩阵阶数为1024时，串行和并行中矩阵乘法耗费时间如下：

串行：

并行：

可看出，阶数为1024时并行花费的时间大约是串行的五分之一。

当改变矩阵阶数，并行和串行所花费时间如下：

	128	256	512	1024	2048
并行	0	31	164	3491	43203
串行	16	100	516	15584	134818

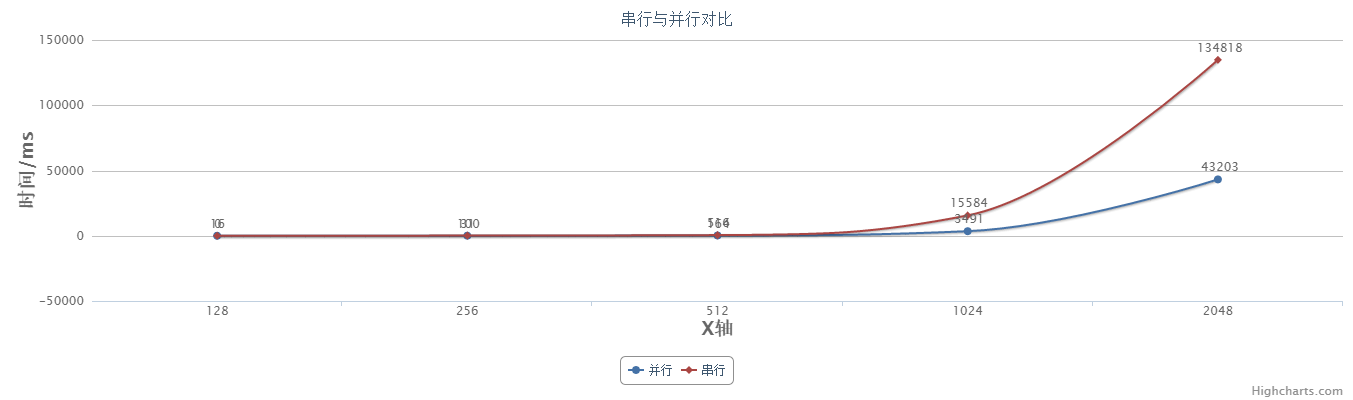
画成折线图如下：

加速比曲线如下（将串行时间除以并行时间）：

从以上图表可以看出当矩阵规模不大（阶数小于500）时，并行算法与串行算法差距不大，当阶数到达1000、2000时，差距就非常明显。而且，并非随着矩阵规模越大，加速比就会越大。在本机硬件条件下，并行线程数为64时，大约在1024附近会有较高加速比。

四 矩阵分块相乘并行算法

将矩阵乘法的计算转化为其各自分块矩阵相乘而后相加，能够有效减少乘数矩阵和被乘数矩阵调入内存的次数，可加快程序执行。

代码如下：

#include <iostream>
#include <omp.h> // OpenMP编程需要包含的头文件
#include <time.h>
#include <stdlib.h>

using namespace std;

#define MatrixOrder 2048
#define FactorIntToDouble 1.1; //使用rand（）函数产生int型随机数，将其乘以因子转化为double型；

double firstParaMatrix [MatrixOrder] [MatrixOrder] = {0.0};
double secondParaMatrix [MatrixOrder] [MatrixOrder] = {0.0};
double matrixMultiResult [MatrixOrder] [MatrixOrder] = {0.0};

/* * * * * * * * * * * * * * * * * * * * * * * * *
* 使用随机数为乘数矩阵和被乘数矩阵赋double型初值 *
* * * * * * * * * * * * * * * * * * * * * * * * */
void matrixInit()
{
    //#pragma omp parallel for num_threads(64)
    for(int row =  ; row < MatrixOrder ; row++ ) {
        for(int col =  ; col < MatrixOrder ;col++){
            srand(row+col);
            firstParaMatrix [row] [col] = ( rand() %  ) * FactorIntToDouble;
            secondParaMatrix [row] [col] = ( rand() %  ) * FactorIntToDouble;
        }
    }
    //#pragma omp barrier
}

void smallMatrixMult (int upperOfRow , int bottomOfRow ,
                      int leftOfCol , int rightOfCol ,
                      int transLeft ,int transRight )
{
    int row=upperOfRow;
    int col=leftOfCol;
    int trans=transLeft;

    #pragma omp parallel for num_threads(64)
    for(int row = upperOfRow ; row <= bottomOfRow ; row++){
        for(int col = leftOfCol ; col < rightOfCol ; col++){
            for(int trans = transLeft ; trans <= transRight ; trans++){
                matrixMultiResult [row] [col] += firstParaMatrix [row] [trans] * secondParaMatrix [trans] [col] ;
            }
        }
    }
    //#pragma omp barrier
}

/* * * * * * * * * * * * * * * * * * * * * * *
* 实现矩阵相乘 *
* * * * * * * * * * * * * * * * * * * * * * * */
void matrixMulti(int upperOfRow , int bottomOfRow ,
                 int leftOfCol , int rightOfCol ,
                 int transLeft ,int transRight )
{
    if ( ( bottomOfRow - upperOfRow ) <  )
        smallMatrixMult ( upperOfRow , bottomOfRow ,
                          leftOfCol , rightOfCol ,
                          transLeft , transRight );

    else
    {
        #pragma omp task
        {
            matrixMulti( upperOfRow , ( upperOfRow + bottomOfRow ) /  ,
                         leftOfCol , ( leftOfCol + rightOfCol ) /  ,
                         transLeft , ( transLeft + transRight ) /  );
            matrixMulti( upperOfRow , ( upperOfRow + bottomOfRow ) /  ,
                         leftOfCol , ( leftOfCol + rightOfCol ) /  ,
                         ( transLeft + transRight ) /  +  , transRight );
        }

        #pragma omp task
        {
            matrixMulti( upperOfRow , ( upperOfRow + bottomOfRow ) /  ,
                         ( leftOfCol + rightOfCol ) /  +  , rightOfCol ,
                         transLeft , ( transLeft + transRight ) /  );
            matrixMulti( upperOfRow , ( upperOfRow + bottomOfRow ) /  ,
                         ( leftOfCol + rightOfCol ) /  +  , rightOfCol ,
                         ( transLeft + transRight ) /  +  , transRight );
        }

        #pragma omp task
        {
            matrixMulti( ( upperOfRow + bottomOfRow ) /  +  , bottomOfRow ,
                         leftOfCol , ( leftOfCol + rightOfCol ) /  ,
                         transLeft , ( transLeft + transRight ) /  );
            matrixMulti( ( upperOfRow + bottomOfRow ) /  +  , bottomOfRow ,
                         leftOfCol , ( leftOfCol + rightOfCol ) /  ,
                         ( transLeft + transRight ) /  +  , transRight );
        }

        #pragma omp task
        {
            matrixMulti( ( upperOfRow + bottomOfRow ) /  +  , bottomOfRow ,
                         ( leftOfCol + rightOfCol ) /  +  , rightOfCol ,
                         transLeft , ( transLeft + transRight ) /  );
            matrixMulti( ( upperOfRow + bottomOfRow ) /  +  , bottomOfRow ,
                         ( leftOfCol + rightOfCol ) /  +  , rightOfCol ,
                         ( transLeft + transRight ) /  +  , transRight );
        }

        #pragma omp taskwait
    }
}

int main()
{
    matrixInit();

    clock_t t1 = clock(); //开始计时；

    //smallMatrixMult( 0 , MatrixOrder - 1 , 0 , MatrixOrder -1 , 0 , MatrixOrder -1 );
    matrixMulti(  , MatrixOrder -  ,  , MatrixOrder - ,  , MatrixOrder - );

    clock_t t2 = clock(); //结束计时
    cout<<"time: "<<t2-t1<<endl; 

    system("pause");

    return ;
}  

　　由于task是openmp 3.0版本支持的特性，尚不支持VS2010，2013，2015,支持的编译器包括GCC,PGI,INTEL等。

程序大致框架与前面并行算法区别不大，只是将计算的矩阵大小约定为512，大于512的矩阵就分块，直到小于512.具体大小可根据实际情况而定。

五  小结

　　本文首先实现基于串行算法的高阶矩阵相乘和基于OpenMP的并行算法的高阶矩阵相乘。接着，对比了128,256,512,1024,2049阶数下，两种算法的耗费时间，并通过表格和曲线图的形式直观表现时间的差别，发现，两种算法并非随着阶数的增大，加速比一直增大，具体原因应该和本机运行环境有关。最后，根据矩阵分块能有效减少数据加载进内存次数，完成了矩阵分块相乘并行算法的代码。考虑到编译环境的限制，未及时将结果运行出来。下一步可装linux虚拟机，使用gcc编译器得出算法的运行时间，进行进一步的分析对比。