Bezier曲线的原理 及 二次Bezier曲线的实现

原文地址：http://blog.csdn.net/jimi36/article/details/7792103

Bezier曲线的原理

Bezier曲线是应用于二维图形的曲线。曲线由顶点和控制点组成，通过改变控制点坐标可以改变曲线的形状。

一次Bezier曲线公式：

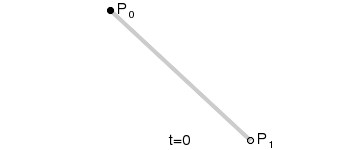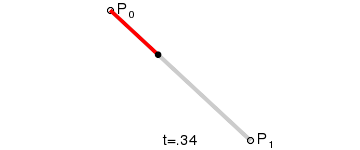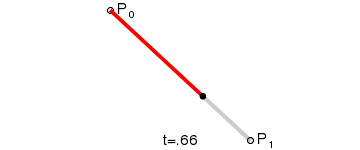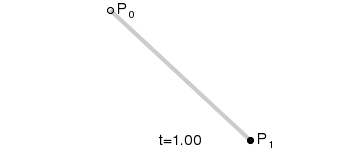
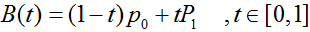
一次Bezier曲线是由P0至P1的连续点，描述的一条线段

二次Bezier曲线公式：

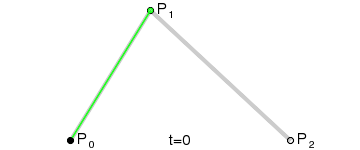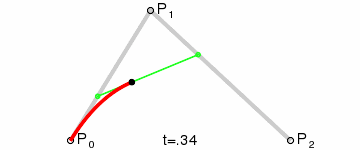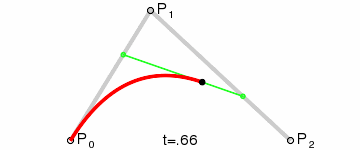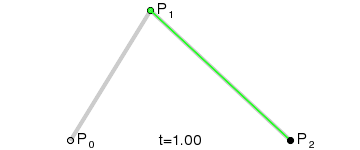
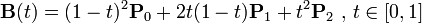
二次Bezier曲线是 P0至P1 的连续点Q0和P1至P2 的连续点Q1 组成的线段上的连续点B(t)，描述一条抛物线。

三次Bezier曲线公式：

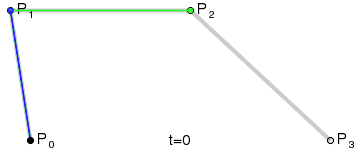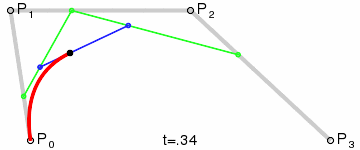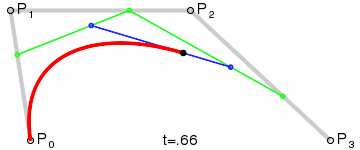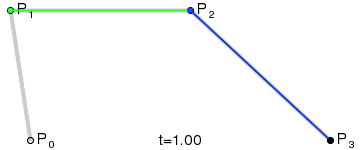
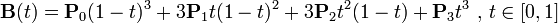
二次Bezier曲线的实现

[cpp] view
plaincopy

1. #ifndef CBEZIERCURVE_H_
2. #define CBEZIERCURVE_H_
3. #include <vector>
4. class CBezierCurve
5. {
6. public:
7. CBezierCurve();
8. ~CBezierCurve();
9. void SetCtrlPoint(POINT& stPt);
10. bool CreateCurve();
11. void Draw(CDC* pDC);
12. private:
13. // 主要算法，计算曲线各个点坐标
14. void CalCurvePoint(float t, POINT& stPt);
15. private:
16. // 顶点和控制点数组
17. std::vector<POINT> m_vecCtrlPt;
18. // 曲线上各点坐标数组
19. std::vector<POINT> m_vecCurvePt;
20. };
21. #endif

[html] view
plaincopy

1. #include <math.h>
2. #include "BezierCurve.h"
3. CBezierCurve::CBezierCurve()
4. {
5. }
6. CBezierCurve::~CBezierCurve()
7. {
8. }
9. void CBezierCurve::SetCtrlPoint(POINT& stPt)
10. {
11. m_vecCtrlPt.push_back(stPt);
12. }
13. void CBezierCurve::CreateCurve()
14. {
15. // 确保是二次曲线，2个顶点一个控制点
16. assert(m_vecCtrlPt.size() == 3);
17. // t的增量， 可以通过setp大小确定需要保存的曲线上点的个数
18. float step = 0.01;
19. for (float t = 0.0; t <= 1.0; t += step)
20. {
21. POINT stPt;
22. CalCurvePoint(t, stPt);
23. m_vecCurvePt.push_back(stPt);
24. }
25. }
26. void CBezierCurve::Draw(CDC* pDC)
27. {
28. // 画出曲线上个点，若不连续可以用直线连接各点
29. int nCount = m_vecCurvePt.size();
30. for (int i = 0; i < nCount; ++i)
31. {
32. pDC->SetPixel(m_vecCurvePt[i], 0x000000);
33. }
34. }
35. void CBezierCurve::CalCurvePoint(float t, POINT& stPt)
36. {
37. // 确保是二次曲线，2个顶点一个控制点
38. assert(m_vecCtrlPt.size() == 3);
39. // 计算曲线点坐标，此为2次算法，改变此处可以实现多次曲线
40. float x = (float)m_vecCtrlPt[0].x * pow(1 - t, 2)   +
41. (float)m_vecCtrlPt[1].x * t * (1 - t) * 2 +
42. (float)m_vecCtrlPt[2].x * pow(t, 2);
43. float y = (float)m_vecCtrlPt[0].y * pow(1 - t, 2)   +
44. (float)m_vecCtrlPt[1].y * t * (1 - t) * 2 +
45. (float)m_vecCtrlPt[2].y * pow(t, 2);
46. stPt.x =x;
47. stPt.y= y;
48. }