Codeforces Round 932 (Div. 2) ABCD

A. Entertainment in MAC

题意：给定字符串 \(S\)，有两种操作，每次操作其中之一：

• 把 \(S\) 变为 \(S\) 的翻转 \(T\)。
• 把 \(S\) 变为 \(S + T\)。

问操作恰好 \(n\) 次能得到的最小字典序，\(n\) 为偶数。

候选字符串的前缀要么是 \(S\)，要么是 \(T\)，前缀相同而长度更长肯定不优，因此 \(ans = min(S, T + S)\)。

void solve() {
	cin >> n >> s;
	t = s;
	ranges::reverse(t);
	if(t < s) cout << (t + s) << '\n';
	else cout << s << '\n';
}

B. Informatics in MAC

题意：给定数组 \(a\)，划分为若干段（大于 \(1\) ），求一种划分方式，使得每段的 \(mex\) 相同，或者不存在。

\(mex\) 相同的两段合并后 \(mex\) 不变。

于是问题转化为：把数组分为两段，使得每段 \(mex\) 相同。

预处理前缀以及后缀 \(mex\)，枚举划分位置。

void solve() {
	int n; cin >> n; vector<int> a(n + 1);

	rep(i, 1, n) cin >> a[i];

	vector<int> pre(n + 1, 0), suf(n + 1, 0);
	set<int> se;
	rep(i, 0, n) se.insert(i);
	rep(i, 1, n) {
		if(se.find(a[i]) != end(se)) {
			se.erase(a[i]);
		}
		pre[i] = *begin(se);
	}
	rep(i, 0, n) se.insert(i);
	per(i, n, 1) {
		if(se.find(a[i]) != end(se)) {
			se.erase(a[i]);
		}
		suf[i] = *begin(se);
	}
	rep(i, 2, n) {
		if(pre[i - 1] == suf[i]) {
			cout << 2 << '\n';
			cout << 1 << ' ' << i - 1 << '\n';
			cout << i << ' ' << n << '\n';
			return;
		}
	}
	cout << -1 << '\n';
}

C. Messenger in MAC

题意：给定 \(n\) 对 \((a, b)\)，选出 \(k\) 对数据并任意排列。

一个长度为 \(k\) 的排列的代价如下定义：

\[\sum_{i=1}^{k} a_{p_i} + \sum_{i=1}^{k - 1} |b_{p_i} - b_{p_{i+1}}|
\]

\(p\) 为各元素在排列中的位置。

在代价不大于 \(m\) 的情况下，最大化 \(k\)。

如果我们已经确定了所选元素，如何最小化代价。

$ \sum a$ 不会随顺序变化。

对于 \(b\)，可以当做遍历数轴上的 \(k\) 个点所走的路程。

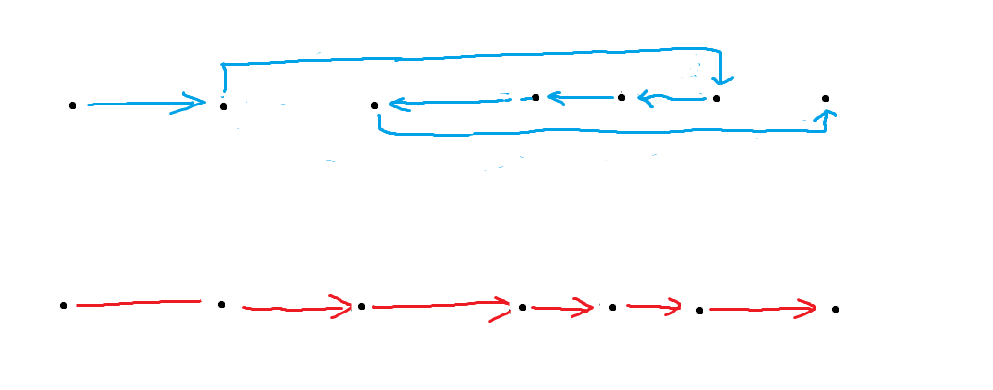
可以直观的看到，对 \(b\) 排序后最优。

因此，所有数先按 \(b\) 排序。

令 \(f[i][j]\) 表示选 \(i\) 个元素，最后一个元素是 \(j\) 的最小代价。

有

\[f[i][j] = f[i - 1][k] + a[j] + (b[j] - b[k]) \ \ \ \ \ \ \ \ k < j
\]

直接转移是 \(O(n^3)\) 的，考虑前缀 \(min\) 优化。

令

\[g[i][j] = min(f[i][k] - b[k]) \ \ \ \ \ \ \ \ 1 \le k \le j
\]

所以

\[f[i][j] = g[i - 1][j - 1] + a[j] + b[j]
\]

struct Node {
	int a, b;
	bool operator < (const Node &o) const {
		return b < o.b;
	}
};

void solve() {
	int n, m; cin >> n >> m;
	vector<Node> t(n + 1);
	rep(i, 1, n) {
		cin >> t[i].a >> t[i].b;
	}
	sort(All(t));

	vector<vector<ll>> f(n + 1, vector<ll>(n + 1, 1e18));
	int ans = 0;

	rep(i, 1, n) {
		if(t[i].a <= m) {
			ans = 1;
		}
		f[1][i] = min(f[1][i - 1], (ll)t[i].a - t[i].b);
	}

	rep(i, 2, n) {
		rep(j, i, n) {
			f[i][j] = f[i - 1][j - 1] + t[j].a + t[j].b;
		}
		rep(j, i, n) {
			if(f[i][j] <= m) {
				ans = i;
			}
			f[i][j] = min(f[i][j - 1], f[i][j] - t[j].b);
		}
	}
	cout << ans << '\n';

}

D. Exam in MAC

题意：给定一个大小为 \(n\) 的不可重集 \(s\) 和整数 \(c\)，统计满足以下所有条件的 \((x, y)\) 对数。

• \(0 \leq x \leq y \leq c\)
• \(x + y\) 不在集合内。
• \(y - x\) 不在集合内。

简单的容斥。

\(Ans = U - \{x + y \in s\} - \{y - x \in s\} + \{x + y \in s\} \cap \{y - x \in s\}\)

最后一部分的交集的充要条件为两元素奇偶性相同，直接统计即可。

void solve() {
	ll n, c; cin >> n >> c;
	ll ans = (c + 2) * (c + 1) / 2;
	int cnt[2] = {0, 0};
	rep(i, 1, n) {
		int x; cin >> x;
		ans -= (x / 2 + 1);
		ans -= (c - x + 1);
		ans += ++ cnt[x & 1];
	}
	cout << ans << '\n';
}