LeetCode1786：从第一个节点出发到最后一个节点的受限路径数（dijkstra + 记忆化搜索）

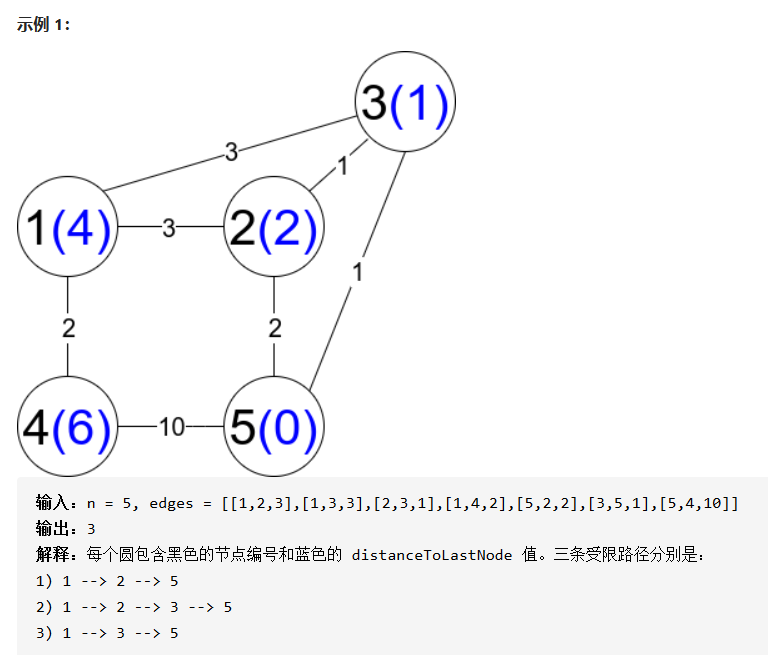
解题思路：比赛的是没读懂题意，这题求的是起点1到n路径序列数，但是路径序列上的相邻两个点 i, i+1 之间应该满足 i、i+1 到终点的最短路low[i] > low[i+1]。

因此需要先以终点开始，跑一遍dijkstra算法，考虑时间复杂度，使用邻接表加优先队列优化。计算得到最短路 low 数组，从起点dfs到终点的路径数量，对于 i 节点，它到终点的路径数 dp[i] = sum(dp[ j ]) ( j 是满足受限条件的下一个节点 j，dp[j] 表示 j 到终点的路径数)；考虑到得数需要模1e7+7，因此可能会重复访问某个节点，因此用dp[i] 数组保存节点 i 到终点的路径数，减少重复的dfs次数。

（ps：用python写的代码似乎有递归深度的限制，在一番折腾无解后，我用栈模拟了 dfs 过程。）

 1 class Node(object):
 2     def __init__(self,x,y):
 3         self.id = x
 4         self.dis = y
 5
 6     def __lt__(self, other):        #定义了<，像C++的重载<运算符
 7         return self.dis<other.dis
 8
 9
10 import heapq
11 class PriorityQueue(object):
12     def __init__(self):
13         self._queue = []
14         self._index = 0
15     def push(self, item, priority):
16         # 传入两个参数，一个是存放元素的数组，另一个是要存储的元素，这里是一个元组。
17         # 由于heap内部默认有小到大排，如果要从大到小排，就要对priority取负数
18         heapq.heappush(self._queue, (priority, self._index, item))
19         self._index += 1
20     def pop(self):
21         return heapq.heappop(self._queue)[-1]
22     def empty(self):
23         return not bool(len(self._queue))
24
25 class Solution(object):
26     def dij(self,n,vec):
27         inf = int(1e9)
28         used = [0]*n
29         low = [inf]*n
30         for i in range(n):
31             low[i] = inf
32         low[-1]=0
33         pq = PriorityQueue()
34         start = n-1
35         pq.push(start,low[n-1])
36         x= 0
37         while not pq.empty():
38             if x>=n:
39                 break
40             now = pq.pop()
41             x+=1
42             #print(now.id)
43             for nxt in vec[now]:
44                 if low[nxt.id] > low[now] + nxt.dis:
45                     low[nxt.id] = low[now] + nxt.dis
46                     pq.push(nxt.id,low[nxt.id])
47
48         return low
49
50     def countRestrictedPaths(self, n, edges):
51         sys.setrecursionlimit(100000)
52         inf = int(1e9)
53         vec = [[] for i in range(n)]
54         for edge in edges:
55             [s1,s2,w] = edge
56             n1,n2 = Node(s2-1,w),Node(s1-1,w)
57             vec[s1-1].append(n1)
58             vec[s2-1].append(n2)
59         #print(dis)
60         low = self.dij(n,vec)
61         #print('aaa')
62         dp = [0]*n
63         used = [0]*n
64         used[0] = 1
65         stack = [0]
66         while len(stack) >0:
67             top = stack.pop()
68             #print(stack)
69             stack.append(top)
70             if top == n-1: #终止条件
71                 _ = stack.pop()
72                 dp[top] = 1
73                 used[top] = 0
74                 continue
75             cnt = 0
76             flag = True
77             for nxt in vec[top]:
78                 i = nxt.id
79                 if low[top] > low[i] and used[i]==0:
80                     if dp[i] == 0: #说明没有访问过，加入栈
81                         #print('aaa',i)
82                         used[i]=1
83                         stack.append(i)
84                         flag = False
85                         break
86                     else:
87                         cnt= (cnt+dp[i])%(inf+7)
88             if not flag: #说明要继续搜索，当前状态不弹出
89                 continue
90             dp[top] = cnt #记忆
91             _ = stack.pop()
92             used[top]=0
93         #print(self.dp)
94         #print(low)
95         return dp[0]