『手撕Vue-CLI』函数柯里化优化代码

开篇

在上一篇文章中，给 nue-cli 添加了拉取版本号的功能，这一次来优化一下代码，使用函数柯里化的方式来优化代码。

实现

函数柯里化

函数柯里化是一种将使用多个参数的一个函数转换成一系列使用一个参数的函数的技术。

在进行改写之前，首先给大家简单介绍一下函数柯里化，写一个简单的例子来演示一下。

function demo(a, b) {
    return a + b;
}

const res = demo(1, 2);
console.log(res);

这是一个简单的函数，接收两个参数，然后返回两个参数的和，除了这种写法其实还可以改写成这样：

function demo(a) {
    return function (b) {
        return a + b;
    };
}

这个时候呢，该如何调用呢？首先是调用 demo 方法，传入一个参数，然后返回一个函数，再调用这个函数，传入另一个参数，最后得到结果。

const res = demo(1)(2);
console.log(res);

了解了这种写法之后，就可以使用函数柯里化来优化代码了。

优化控制台加载效果

为什么是要优化控制台加载效果呢？因为我发现后续可能对控制台加载效果的需求会比较多，所以就把这个功能单独提取出来。

例如像之前拉取模板名称，拉取版本号，拉取模板等等，都需要控制台加载效果，所以就把这个功能单独提取出来，以后需要的时候直接调用就可以了。

const waitLoading = async ( message, fn) => {
    const spinner = ora(message).start();
    const result = await fn();
    spinner.succeed(`${message} successfully`);
    return result;
}

这个函数接收两个参数，第一个参数是 message，第二个参数是 fn，message 是控制台加载效果的提示信息，fn 是一个异步函数，这个函数会返回一个 Promise 对象，然后在函数内部调用 ora，显示加载效果，然后调用 fn，等待 fn 执行完毕，最后关闭加载效果。

改造获取模板名称

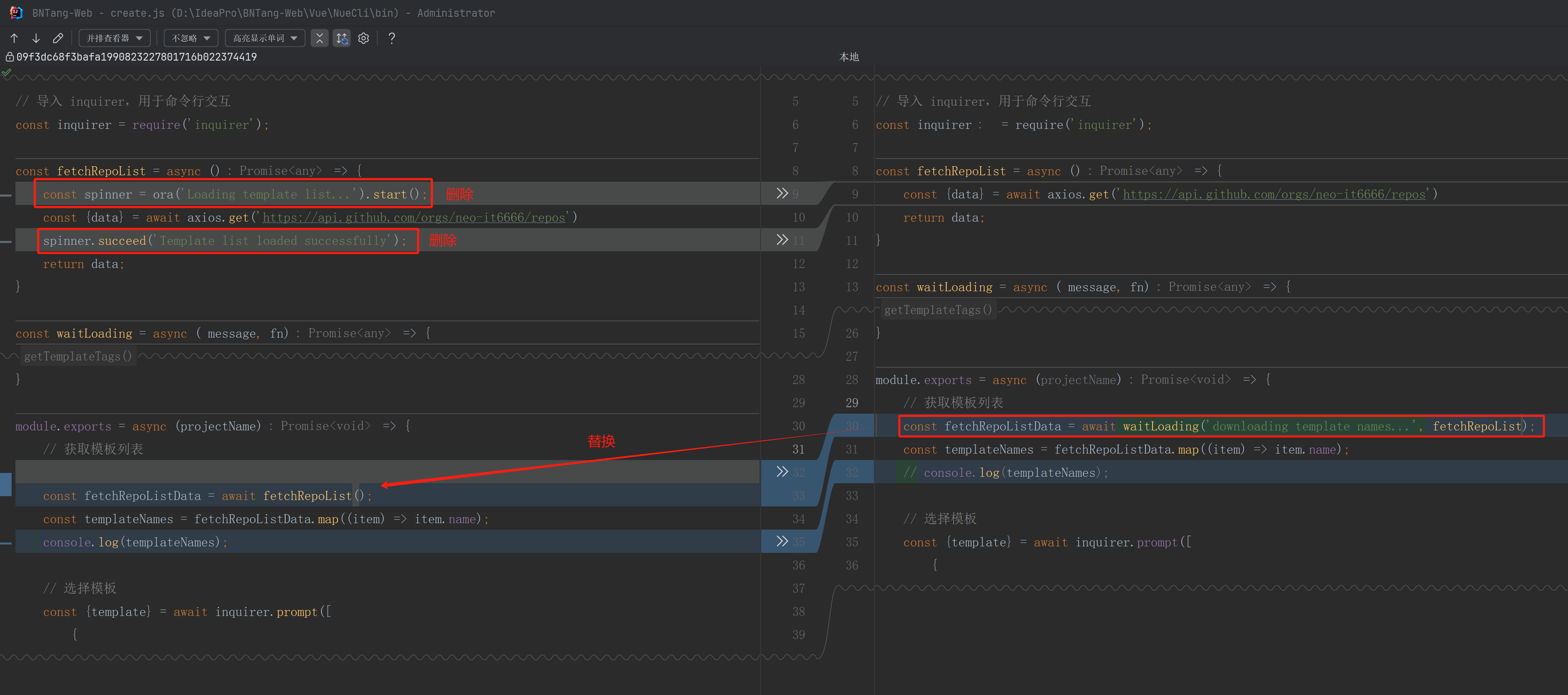
主要就是将 fetchRepoList 中通过 ora 显示加载效果的代码删除掉，然后调用 waitLoading 函数，将 fetchRepoList 传入进去，这样就改造完成了。

const fetchRepoListData = await waitLoading('downloading template names...', fetchRepoList)();

改造获取版本号

这里改造其实是一样的，不过这里有一个小问题，就是 getTemplateTags 这个函数是需要传入一个参数的，所以需要对 waitLoading 进行改造。

const waitLoading =  ( message, fn) => async (...args) => {
    const spinner = ora(message).start();
    const result = await fn(...args);
    spinner.succeed(`${message} successfully`);
    return result;
}

这回的 waitLoading 方法与之前的不同地方就是在添加了一个 ...args 参数，这个参数是用来接收 fn 函数的参数的，然后在调用 fn 的时候将参数传入进去。

接下来就是改造调用 getTemplateTags 的地方了。

const fetchTemplateTags = await waitLoading('downloading template tags...', getTemplateTags)(template);

由于改造了 waitLoading 方法，之前调用 waitLoading 方法的地方也需要进行改造，就是多加一个调用过程。

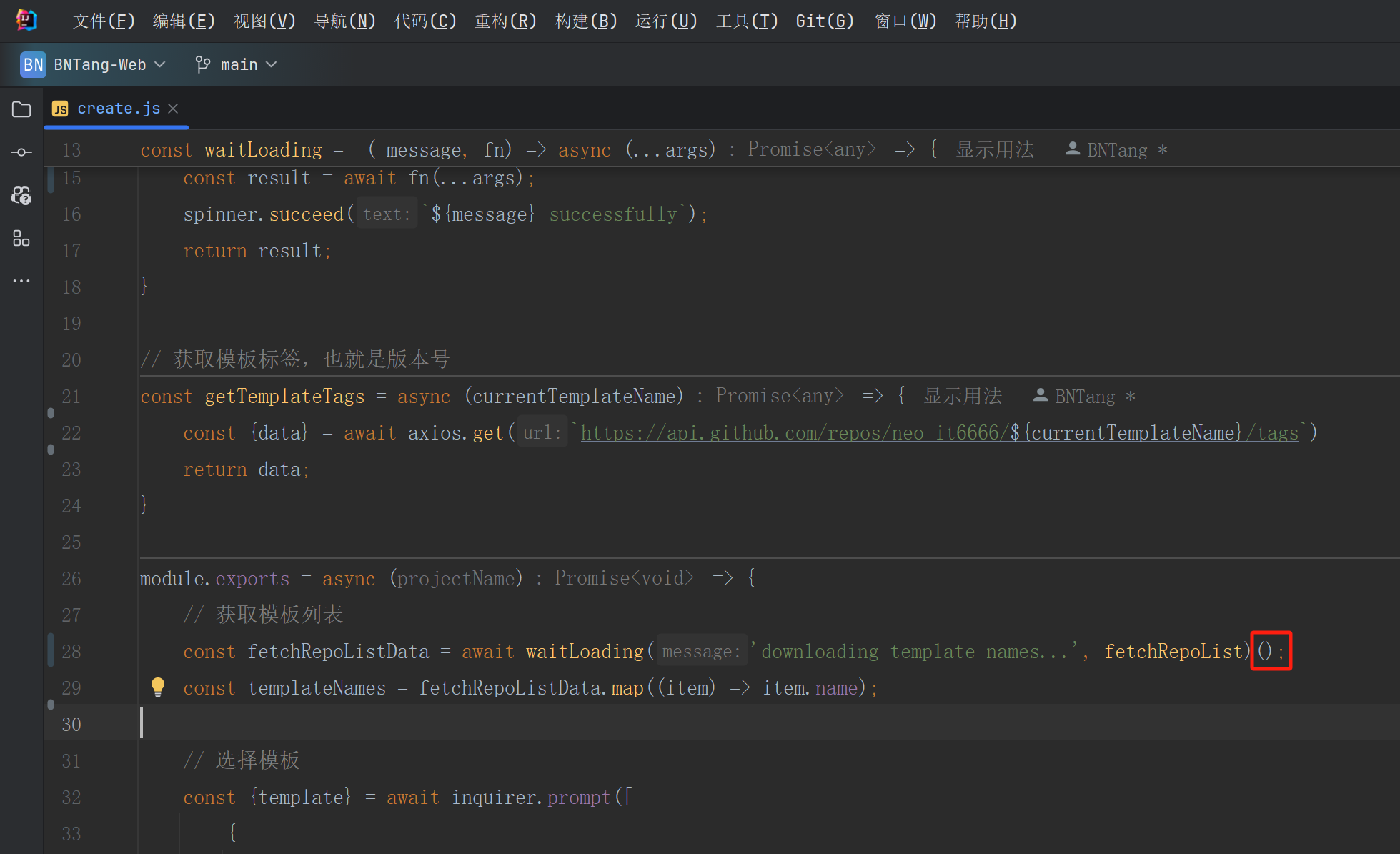
好，大致就是这样，本篇文章就到这里了，下一篇文章继续完善 nue-cli。