LuoguP2698 【[USACO12MAR]花盆Flowerpot】

题目描述

首先我们简化一下题意：

要找一段区间[L,R]，使区间[L,R]内元素最大值减最小值大于等于D。

做法：

首先很容易想到采用二分，分什么呢？

我们二分区间长度为mid

这个时候，检验就成为了我们的目标

最暴力的检验就是枚举左端点，在区间内找最大和最小，有一个max-min>=D

让我们模拟一下：

假如mid=2：

(1) [1,3]

(2) [2,4]

(3) [3 5]

(4) .....

我们震惊的发现：P1886 滑动窗口

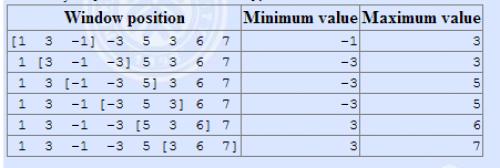
这貌似有点相似

于是正解出现了

正解：

二分区间长度为mid，检验时用单调队列维护区间最大最小值，复杂度nlogn，更多细节见代码：

代码时间到：

#include<bits/stdc++.h>
using namespace std;
int n,D,l,r;
struct WATER{
    int x,y;
}p[];
int ans=;
int q1[],q2[];
int p1[],p2[];
int head1=,tail1=,head2=,tail2=;
bool check(int k){
    int L=;
    q1[]=p[].y;p1[]=p[].x;
    q2[]=p[].y;p2[]=p[].x;
    head1=,tail1=,head2=,tail2=;
    for(int i=;i<=n;i++){
        while((p[i].x-p[L].x)>k) L++;
        while(p1[head1]<p[L].x&&head1<=tail1)
              head1++;
        while(p2[head2]<p[L].x&&head2<=tail2)
              head2++;
        while(q1[tail1]<=p[i].y&&head1<=tail1)
              tail1--;
        p1[++tail1]=p[i].x;q1[tail1]=p[i].y;
        while(q2[tail2]>=p[i].y&&head2<=tail2)
              tail2--;
        p2[++tail2]=p[i].x;q2[tail2]=p[i].y;
        if((q1[head1]-q2[head2])>=D) return ;
    }
    return ;
}
bool cmp(WATER a,WATER b){
    return a.x<b.x;
}
int main(){
    scanf("%d%d",&n,&D);
    for(int i=;i<=n;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    l=,r=;
    sort(p+,p+n+,cmp);
    while(l<=r){
        int mid=(l+r)/;
        if(check(mid)){
            r=mid-;
            ans=min(ans,mid);
        }
        else l=mid+;
    }
    if(ans==) printf("-1");
    else printf("%d",ans);
    return ;
}