Python入门篇-数据结构堆排序Heap Sort

　　　　　　　　　　Python入门篇-数据结构堆排序Heap Sort

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　作者：尹正杰

版权声明：原创作品，谢绝转载！否则将追究法律责任。

一.堆Heap

　　堆是一个完全二叉树
　　每个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆
　　每个非叶子结点都要小于或者等于其左右孩子结点的值称为小顶堆
　　根结点一定是大顶堆中的最大值，一定是小顶堆中的最小值

二.大顶堆

　　完全二叉树的每个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆
　　根结点一定是大顶堆中的最大值

三.小顶堆

　　完全二叉树的每个非叶子结点都要小于或者等于其左右孩子结点的值称为小顶堆
　　根结点一定是小顶堆中的最小值

四.构建完全二叉树

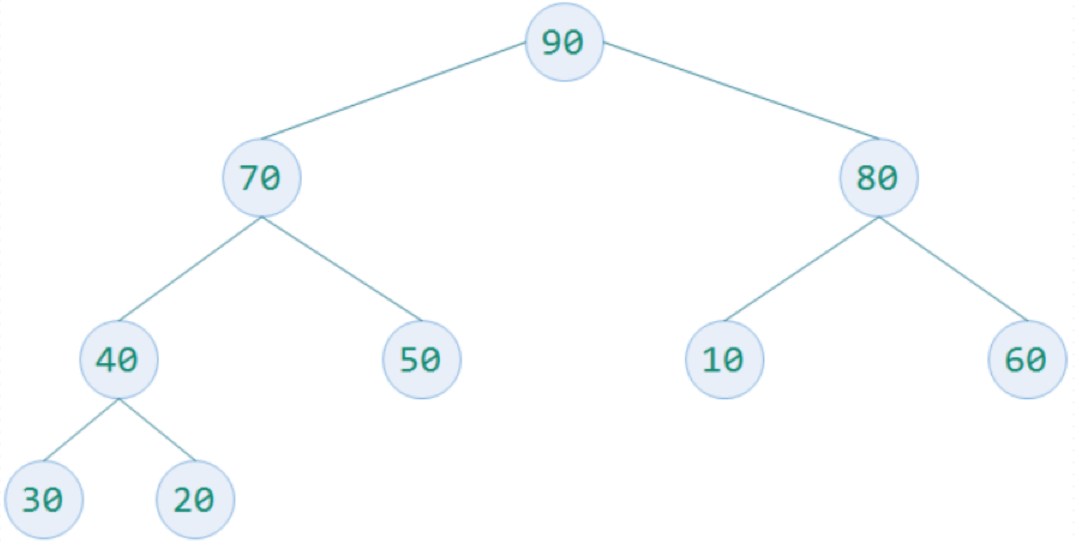
　　待排序数字为30,,,,,,,,90.
　　构建一个完全二叉树存放数据，并根据性质5对元素编号，放入顺序的数据结构中.
　　构造一个列表为[,,,,,,,,,].

五.构建大顶堆 

1>.核心算法

　　度数为2的结点A，如果它的左右孩子结点的最大值比它大的，将这个最大值和该结点交换.
　　度数为1的结点A，如果它的左孩子的值大于它，则交换.
　　如果结点A被交换到新的位置，还需要和其孩子结点重复上面的过程.

2>.起点结点的选择

　　从完全二叉树的最后一个结点的双亲结点开始，即最后一层的最右边叶子结点的父结点开始.
　　结点数为n，则起始结点的编号为n//2（性质5）.

3>.下一个结点的选择

　　从起始结点开始向左找其同层结点，到头后再从上一层的最右边结点开始继续向左逐个查找，直至根结点.

4>.大顶堆的目标

　　确保每个结点的都比左右结点的值大.

5>.排序

　　将大顶堆根结点这个最大值和最后一个叶子结点交换，那么最后一个叶子结点就是最大值，将这个叶子结点排除在待排序结点之外.
　　从根结点开始（新的根结点），重新调整为大顶堆后，重复上一步.
　　堆顶和最后一个结点交换，并排除最后一个结点.

 6>.代码实现

 #！/usr/bin/env python
 #_*_coding:utf-8_*_
 #@author :yinzhengjie
 #blog:http://www.cnblogs.com/yinzhengjie/tag/python%E8%87%AA%E5%8A%A8%E5%8C%96%E8%BF%90%E7%BB%B4%E4%B9%8B%E8%B7%AF/
 #EMAIL:y1053419035@qq.com

 import math

 def print_tree(array):
     index = 1
     depth = math.ceil(math.log2(len(array)))        #因为补0了，不然应该是math.ceil(math.log2(len(array) + 1)
     sep = " "
     for i in range(depth):
         offset = 2 ** i
         print(sep * (2 **(depth - i -1)-1),end="")
         line = array[index:index + offset]
         for j,x in enumerate(line):
             print("{:>{}}".format(x,len(sep)),end="")
             interval = 0 if i == 0 else 2 ** (depth - i) -1
             if j < len(line) - 1:
                 print(sep * interval,end="")
             index += offset
             print()

 #为了和编码对应，增加一个无用的0在首位
 origin = [0,30,20,80,40,50,10,60,70,90]
 total = len(origin) - 1     #初始化排序元素个数，即n
 print(origin)

 print_tree(origin)
 print_tree("=" * 50)

 def heap_adjust(n,i,array:list):
     """
         调整当前结点（核心算法）
         调整的节点的起点在n//2，保证所有的调整的结点都有孩子结点
     :param n: 待比较数个数
     :param i: 当前结点的下标
     :param array:待排序的数据
     :return:
     """
     while 2 * i <= n:
         #孩子结点判断2i位左孩子，2i+1为右孩子
         lchile_index = 2 * i
         max_child_index = lchile_index              #n = 2i
         if n > lchile_index and array[lchile_index +1] > array[lchile_index]:       #n > 2i说明还有右孩子
             max_child_index = lchile_index + 1      #n = 2i +1

         #和子树的根结点比较
         if array[max_child_index] > array[i]:
             array[i],array[max_child_index] = array[max_child_index],array[i]
             i = max_child_index                     #被比较后，需要判断是否需要调整
         else:
             break

 #构建大顶推，大根堆
 def max_heap(total,array:list):
     for i in range(total//2,0,-1):
         heap_adjust(total,i,array)
     return array

 print_tree(max_heap(total,origin))
 print_tree("=" * 50)

 #排序
 def sort(total,array:list):
     while total > 1:
         array[1],array[total] = array[total],array[1]           #堆顶和最后一个结点交换
         total -= 1
         if total == 2 and array[total] >= array[total -1]:
             break
         heap_adjust(total,1,array)
     return array

 print_tree(sort(total,origin))
 print_tree(origin)
   

六.总结

是利用堆性质的一种选择排序，在堆顶选出最大值或者最小值
　　时间复杂度.
　　堆排序的时间复杂度为O(nlogn).
　　由于堆排序对原始记录的排序状态并不敏感，因此它无论是最好、最坏和平均时间复杂度均为O(nlogn).

1>.空间复杂度

　　只是使用了一个交换用的空间，空间复杂度就是O().

2>.稳定性

　　不稳定的排序算法.