PHP实现二叉树的深度优先遍历（前序、中序、后序）和广度优先遍历（层次）

前言：

深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：

• 前序遍历：根节点->左子树->右子树
• 中序遍历：左子树->根节点->右子树
• 后序遍历：左子树->右子树->根节点

广度优先遍历：又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。

例如对于一下这棵树：

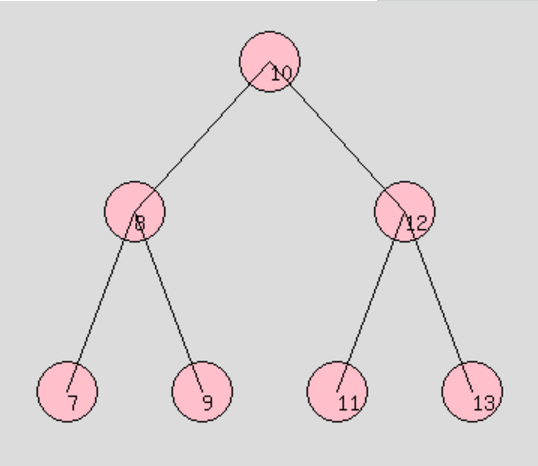
深度优先遍历：

• 前序遍历：10 8 7 9 12 11 13
• 中序遍历：7 8 9 10 11 12 13
• 后序遍历：7 9 8 11 13 12 10

广度优先遍历：

• 层次遍历：10 8 12 7 9 11 13

二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

代码示例：

 <?php
 header("Content-type: text/html; charset=utf-8");
 class Node
 {
     public $value;
     public $left;
     public $right;

     public function __construct($value)
     {
         $this->value = $value;
     }
 }

 class Tree
 {
     /**
      * 先序遍历(递归方法)
      */
     public function recursion_preorder($root)
     {
         static $res = array();
         if (!is_null($root))
         {
             $function = __FUNCTION__;
             $res[] = $root->value;
             $this->$function($root->left);
             $this->$function($root->right);
         }
         return $res;
     }

     /**
      * 中序遍历(递归方法)
      */
     public function recursion_midorder($root)
     {
         static $res = array();
         if(!is_null($root))
         {
             $function = __FUNCTION__;
             $this->$function($root->left);
             $res[] = $root->value;
             $this->$function($root->right);
         }
         return $res;
     }

     /**
      * 后序遍历(递归方法)
      */
     public function recursion_postorder($root)
     {
         static $res = array();
         if (!is_null($root))
         {
             $function = __FUNCTION__;
             $this->$function($root->left);
             $this->$function($root->right);
             $res[] = $root->value;
         }
         return $res;
     }

     /**
      * 先序遍历(非递归)
      */
     public function preorder($node)
     {
         $res = array();
         $stack = new splstack();
         while(!is_null($node) || !$stack->isEmpty())
         {
             while(!is_null($node))//节点不为空就入栈
             {
                 $stack->push($node);
                 $res[] = $node->value;
                 $node = $node->left;
             }
             $node = $stack->pop();
             $node = $node->right;
         }
         return $res;
     }

     /**
      * 中序遍历(非递归)
      */
     public function midorder($node)
     {
         $res = array();
         $stack = new splstack();
         while(!is_null($node) || !$stack->isEmpty())
         {
             while(!is_null($node))
             {
                 $stack->push($node);
                 $node = $node->left;
             }
             $node = $stack->pop();
             $res[] = $node->value;
             $node = $node->right;
         }
         return $res;
     }

     /**
      * 后序遍历(非递归)
      */
     public function postorder($node)
     {
         $stack = new splstack();
         $outstack = new splstack();

         $stack->push($node);
         while(!$stack->isEmpty())
         {
             $center_node = $stack->pop();
             $outstack->push($center_node);//最先压入根节点，最后输出
             if(!is_null($center_node->left))
             {
                 $stack->push($center_node->left);
             }
             if(!is_null($center_node->right))
             {
                 $stack->push($center_node->right);
             }
         }

         $res = array();
         while(!$outstack->isEmpty())
         {
             $node = $outstack->pop();
             $res[] = $node->value;
         }
         return $res;
     }

     /**
      * 广度优先遍历(层次遍历、非递归)
      */
     public function level_order($node)
     {
         $res = array();
         $queue = new splqueue();
         $queue->enqueue($node);
         while(!$queue->isEmpty())
         {
             $node = $queue->dequeue();
             $res[] = $node->value;
             if(!is_null($node->left))
             {
                 $queue->enqueue($node->left);
             }
             if(!is_null($node->right))
             {
                 $queue->enqueue($node->right);
             }
         }
         return $res;
     }
 }

 $a = new Node(10);
 $b = new Node(8);
 $c = new Node(12);
 $d = new Node(7);
 $e = new Node(9);
 $f = new Node(11);
 $g = new Node(13);

 $a->left = $b;
 $a->right = $c;
 $b->left = $d;
 $b->right = $e;
 $c->left = $f;
 $c->right = $g;

 $tree = new Tree();
 $res = $tree->recursion_preorder($a);
 echo "先序遍历结果(递归)：" . implode('-', $res) . "<br/>";

 $res = $tree->preorder($a);
 echo "先序遍历结果(非递归)：" . implode('-', $res) . "<br/>";

 $res = $tree->recursion_midorder($a);
 echo "中序遍历结果(递归)：" . implode('-', $res) . "<br/>";

 $res = $tree->midorder($a);
 echo "中序遍历结果(非递归)：" . implode('-', $res) . "<br/>";

 $res = $tree->recursion_postorder($a);
 echo "后序遍历结果(递归)：" . implode('-', $res) . "<br/>";

 $res = $tree->postorder($a);
 echo "后序遍历结果(非递归)：" . implode('-', $res) . "<br/>";

 $res = $tree->level_order($a);
 echo "层次遍历结果(非递归)：" . implode('-', $res) . "<br/>";