hihoCoder 1184 连通性二·边的双连通分量

#1184 : 连通性二·边的双连通分量

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在基本的网络搭建完成后，学校为了方便管理还需要对所有的服务器进行编组，网络所的老师找到了小Hi和小Ho，希望他俩帮忙。

老师告诉小Hi和小Ho：根据现在网络的情况，我们要将服务器进行分组，对于同一个组的服务器，应当满足：当组内任意一个连接断开之后，不会影响组内服务器的连通性。在满足以上条件下，每个组内的服务器数量越多越好。

比如下面这个例子，一共有6个服务器和7条连接：

其中包含2个组，分别为{1,2,3},{4,5,6}。对{1,2,3}而言，当1-2断开后，仍然有1-3-2可以连接1和2；当2-3断开后，仍然有2-1-3可以连接2和3；当1-3断开后，仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。

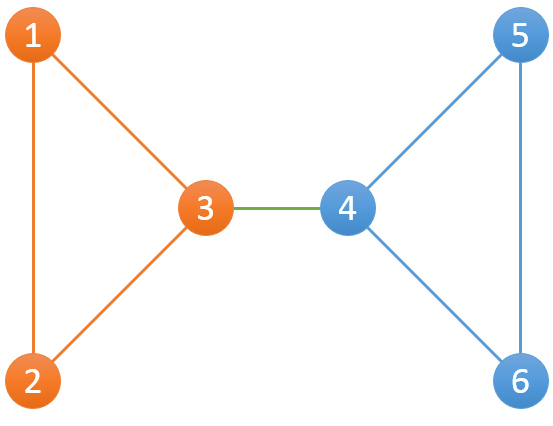
老师把整个网络的情况告诉了小Hi和小Ho，小Hi和小Ho要计算出每一台服务器的分组信息。

提示：边的双连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2..M+1行：2个正整数，u,v。表示存在一条边(u,v)，连接了u,v两台服务器。1≤u<v≤N

保证输入所有点之间至少有一条连通路径。

输出

第1行：1个整数，表示该网络的服务器组数。

第2行：N个整数，第i个数表示第i个服务器所属组内，编号最小的服务器的编号。比如分为{1,2,3},{4,5,6}，则输出{1,1,1,4,4,4}；若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}

样例输入

6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6

样例输出

2
1 1 1 4 4 4

题目链接：Hihocoder 1184

求无向图的双连通分量，一般做法是先求出桥，然后把桥边标记删除，再DFS出所有连通块，这样每一个连通块便都是在一个边双连通分量里了。

代码：

#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int,int> pii;
typedef long long LL;
const double PI=acos(-1.0);
const int N=200010;
const int M=1e5+7;
struct edge
{
    int to,nxt;
    int id,flag;
};
edge E[M<<1];
int head[N],tot;
int dfn[N],low[N],st[N],ts,top;
bool ins[N];
int rev[N];

void init()
{
    CLR(head,-1);
    tot=0;
    CLR(dfn,0);
    CLR(low,0);
    ts=top=0;
    CLR(ins,false);
    CLR(rev,INF);
    bridge=0;
}
inline void add(int s,int t,int id)
{
    E[tot].to=t;
    E[tot].flag=0;
    E[tot].id=id;
    E[tot].nxt=head[s];
    head[s]=tot++;
}
void Tarjan(int u,int id)
{
    dfn[u]=low[u]=++ts;
    ins[u]=1;
    st[top++]=u;
    int i,v;
    for (i=head[u]; ~i; i=E[i].nxt)
    {
        v=E[i].to;
        if(E[i].id==id)
            continue;
        if(!dfn[v])
        {
            Tarjan(v,E[i].id);
            low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u])
            {
                E[i].flag=true;
                E[i^1].flag=true;
            }
        }
        else if(ins[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        do
        {
            v=st[--top];
            ins[v]=0;
        }while (u!=v);
    }
}
void dfs(int u,int pre)
{
    rev[u]=min(rev[pre],u);
    ins[u]=1;
    for (int i=head[u]; ~i; i=E[i].nxt)
    {
        if(E[i].flag)
            continue;
        if(!ins[E[i].to])
            dfs(E[i].to,u);
    }
}
int main(void)
{
    int n,m,a,b,i;
    while (~scanf("%d%d",&n,&m))
    {
        init();
        for (i=0; i<m; ++i)
        {
            scanf("%d%d",&a,&b);
            add(a,b,i);
            add(b,a,i);
        }
        CLR(ins,false);
        for (i=1; i<=n; ++i)
            if(!dfn[i])
                Tarjan(i,-1);
        int sz=1;
        for (i=1; i<=n; ++i)
            if(!ins[i])
                dfs(i,i);
        printf("%d\n",bridge+1);
        for (i=1; i<=n; ++i)
            printf("%d%s",rev[i],i==n?"\n":" ");
    }
    return 0;
}