c/c++ 二叉排序树

c/c++ 二叉排序树

概念：

左树的所有节点的值（包括子节点）必须小于中心节点，右树所有节点的值（包括子节点）必须大于中心节点。

不允许有值相同的节点。

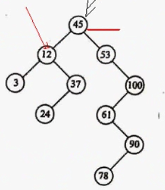
二叉排序树的特点：

• 中序遍历后，就是从小到大排序了。
• 根节点的最左边的值，就是树中最小的值。
• 根节点的最右边的值，就是树中最大的值。

创建二叉排序树的思路：

• 用递归的方式
• 和根节点比较大小
• 比根节点小的话，用递归去和根节点的左节点比较，至到找到合适的位置
• 比根节点大的话，用递归去和根节点的右节点比较，至到找到合适的位置

二叉排序树的一些实用函数

init_bst	初始化二叉排序树
insert_bst_tree	插入树的节点
min	求树中最小节点
max	求树中最大节点
sort	排序二叉树（中序遍历就是从小到大排序了）
remove_bst	删除节点

删除节点

pattern1：要被删除的节点是root节点

• 方案1：用根节点左树中的最大的节点作为新的根节点

删除45

• 方案2：用根节点又树中的最小的节点作为新的根节点

删除45

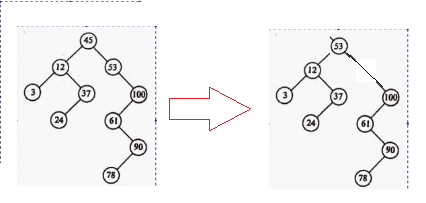
pattern2：要被删除的节点是其父节点的左树，并且要被删除的节点有右树

删除12

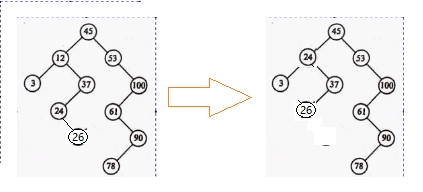
pattern3：要被删除的节点是其父节点的左树，并且要被删除的节点无右树

删除12

pattern4：要被删除的节点是其父节点的右树，并且要被删除的节点无左树

删除53

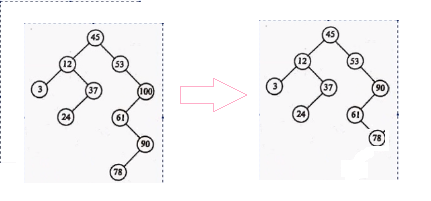
pattern5：要被删除的节点是其父节点的右树，并且要被删除的节点有左树

删除100

bst.h

#ifndef __BST__
#define __BST__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>

#define T int
#define FALSE 0
#define TRUE 1
#define BOOL int

typedef struct BSTNode{
  T data;
  struct BSTNode* left;
  struct BSTNode* right;
}BSTNode;

typedef struct BST{
  BSTNode* root;
}BST;

//初始化二叉排序树
void init_bst(BST* bst);
//插入树的节点
BOOL insert_bst_node(BSTNode** t, T x);
BOOL insert_bst_tree(BST* bst, T x);
//求树中最小节点
T min(BST* bst);
//求树中最大节点
T max(BST* bst);
//排序
void sort(BST* bst);
//查找父节点
BSTNode* get_parent(BST* bst, BSTNode* tar);
//删除节点
BOOL remove_bst(BST* bst, T key);
//搜索节点
BSTNode* search_bst(BST* bst, T key);
//搜索节点
BSTNode* search_bst1(BST* bst, T key);
//清空树
void clear_bst(BST* bst);

#endif

bst.c

#include "bst.h"

//初始化二叉排序树
void init_bst(BST* bst){
  bst->root = NULL;
}

//插入树的节点
BOOL insert_bst_node(BSTNode** t, T x){
  if(*t == NULL){
    *t = (BSTNode*)malloc(sizeof(BSTNode));
    assert(NULL != *t);
    (*t)->data  = x;
    (*t)->left  = NULL;
    (*t)->right = NULL;
    return TRUE;
  }
  else if(x < (*t)->data){
    insert_bst_node(&((*t)->left), x);
  }
  else if(x > (*t)->data){
    insert_bst_node(&((*t)->right), x);
  }
  return FALSE;
}
BOOL insert_bst_tree(BST* bst, T x){
  return insert_bst_node(&(bst->root), x);
}

//求树中最小节点
T min_node(BSTNode* t){
  while(t->left != NULL)
    t = t->left;
  return t->data;
}
T min(BST* bst){
  assert(bst->root != NULL);
  return min_node(bst->root);
}
//求树中最大节点
T max_node(BSTNode* t){
  while(t->right != NULL){
    t = t->right;
  }
  return t->data;
}
T max(BST* bst){
  assert(bst->root != NULL);
  return max_node(bst->root);
}
//二叉树中序排序
void sort_node(BSTNode* t){
  if(NULL == t){
    return;
  }else{
    sort_node(t->left);
    printf("%d ", t->data);
    sort_node(t->right);
  }
}
void sort(BST* bst){
  assert(NULL != bst->root);
  sort_node(bst->root);
}
//搜索节点
BSTNode* search_node(BSTNode* t, T key){
  if(NULL == t || t->data == key){
    return t;
  }
  else{
    BSTNode* p;
    p = search_node(t->left, key);
    if(NULL == p){
      p = search_node(t->right, key);
    }
    return p;
  }
}
BSTNode* search_bst(BST* bst, T key){
  return search_node(bst->root, key);
}
BSTNode* search_node1(BSTNode* t, T key){
  if(NULL == t || t->data == key){
    return t;
  }
  else{
    if(key < t->data){
      search_node1(t->left, key);
    }
    else{
      search_node1(t->right, key);
    }
  }
}
BSTNode* search_bst1(BST* bst, T key){
  return search_node1(bst->root, key);
}
//清空树
void clear_node(BSTNode** t){
  if(NULL != *t){
    clear_node(&((*t)->left));
    clear_node(&((*t)->right));
    free(*t);
    *t = NULL;
  }
}
void clear_bst(BST* bst){
  clear_node(&bst->root);
}

//查找父节点
BSTNode* get_parent_node(BSTNode* t, BSTNode* tar){
  if(NULL == t || NULL == tar)return NULL;
  if(t->left == tar || t->right == tar){
    return t;
  }
  else{
    BSTNode* p = NULL;
    p = get_parent_node(t->left, tar);
    if(NULL == p){
      p = get_parent_node(t->right, tar);
    }
    return p;
  }
}
BSTNode* get_parent(BST* bst, BSTNode* tar){
  return get_parent_node(bst->root, tar);
}
BOOL remove_bst(BST* bst, T key){

  BSTNode* tar = search_bst(bst, key);
  //树为空或者要删除的节点不存在，返回失败
  if(bst->root == NULL || NULL == tar) return FALSE;

  BSTNode* parent = get_parent(bst, tar);
  //因为要被删除的顶点有左子节点，所以要找到以左子节点为根的右子节点中值最大的
  BSTNode* X = NULL;
  if(NULL != tar->left){
    X = tar->left;
    while(X->right != NULL){
      X = X->right;
    }

    //因为要被删除的顶点的左子节点,有右子节点，所以要找到最大的
    if(X != tar->left){
      //找到最大节点的父节点
      BSTNode* X1 = get_parent(bst, X);
      //最大节点的父节点的右边指向最大节点的左边
      X1->right = X->left;

      //最大节点的左边代替被删除节点的左边，右边代替右边
      X->left = tar->left;
      X->right = tar->right;
    }
    //因为要被删除的顶点的左子节点,没有右子节点，所以它就是最大的
    else{
      X->right = tar->right;
    }
  }
  //因为要被删除的顶点没有左子节点，所以要找到以右子节点为根的左子节点中值最小的
  else{
    X = tar->right;
    //要被删除的节点既没有左节点，也没有右节点
    if(NULL == X){
      //找到父节点
      BSTNode* X2 = get_parent(bst, X);
      //要被删除的节点不是根节点
      if(parent != NULL){
	//要被删除的顶点在父节点的左边
	if(tar->data < parent->data){
	  parent->left = X;
	}
	//要被删除的顶点在父节点的右边
	else{
	  parent->right = X;
	}
      }
      else{
	bst->root = NULL;
      }
      free(tar);
      return TRUE;
    }
    while(X->left != NULL){
      X = X->left;
    }
    //因为要被删除的顶点的右子节点,有左子节点，所以要找到最小的
    if(X != tar->right){
      //找到最小节点的父节点
      BSTNode* X1 = get_parent(bst, X);
      //最小节点的父节点的左边指向最小节点的右边
      X1->left = X->right;

      //最小节点的左边代替被删除节点的左边，右边代替右边
      X->right = tar->right;
      X->left = tar->left;
    }
  }
  //要被删除的节点不是根节点
  if(parent != NULL){
    //要被删除的顶点在父节点的左边
    if(tar->data < parent->data){
      parent->left = X;
    }
    //要被删除的顶点在父节点的右边
    else{
      parent->right = X;
    }
  }
  else{
    bst->root = X;
  }
  free(tar);
}

bstmain.c

#include "bst.h"

int main(){
  BST bst;
  init_bst(&bst);

  //patten1 目标节点是root,root没有右子节点，左子节点中有右子节点
  //T ar[] = {45,12,3,37,24,38};
  //patten2 目标节点是root,root没有右子节点，左子节点中没有右子节点
  //T ar[] = {45,12,3};
  //patten3 目标节点是root,只有root节点
  //T ar[] = {45};
  //patten4 目标节点是root,root有右子节点，右子节点中没有左子节点
  //T ar[] = {45,12,53,3,37,100,24};
  //patten5 目标节点是root,root有右子节点，右子节点中有左子节点
  //T ar[] = {45,12,53,3,37,100,24,61,90,78};

  //patten6 目标节点(8)不是root,目标节点有左子节点，左子节点没有右边
  //T ar[] = {45,12,53,3,27,2,4,24,1,6,5,8,7};
  //patten7 目标节点(12)不是root,目标节点有左子节点，左子节点有右边
  //T ar[] = {45,12,53,3,27,2,4,24,1,6,5,8,7};
  //patten8 目标节点(120)不是root,目标节点没有左子节点，右子节点没有左边
  T ar[] = {45,12,53,3,37,52,100,2,4,24,51,61,120,1,6,90,130,5,8,78,126,140,7,124,127,125};

  //T ar[] = {45,12,53,3,37,100,24,61,90,78};
  //T ar[] = {45,3,4,12,53};
  int n = sizeof(ar) / sizeof(T);
  for(int i = 0; i < n; ++i){
    insert_bst_tree(&bst, ar[i]);
  }

  sort(&bst);
  printf("\n");

  //删除节点
  remove_bst(&bst, 45);
  sort(&bst);
  printf("\n");

  clear_bst(&bst);
}

完整代码

编译方法：gcc -g bst.c bstmain.c