MT【305】丹德林双球

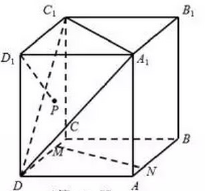
如图.在正方体$ABCD-A_1B_1C_1D_1$中,点$M,N$分别是直线$CD,AB$上的动点,点$P$是$\Delta A_1C_1D_1$内的动点(不包括边界),记直线$DP$与$MN$所成角为$\theta$,若$\theta$的最小值为$\dfrac{\pi}{3}$,则点$P$的轨迹为（      ）
A.圆的一部分

B.椭圆的一部分

C.抛物线的一部分

D.双曲线的一部分

答案 B

分析:“二面角最大,线面角最小”.从而我们知道$D_1P$与底面$ABCD$所成的角为$\dfrac{\pi}{3}$,故$P$在以$DD_1$为轴的圆锥面上,所以$P$的轨迹为面$A_1C_1D$截圆锥所得的曲线.

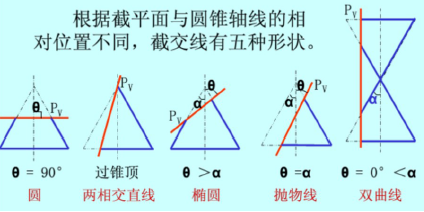
$e=\dfrac{cos\theta}{\cos\alpha}=\dfrac{\dfrac{\sqrt{6}}{3}}{cos\dfrac{\pi}{6}}=\dfrac{2\sqrt{2}}{3}\in(0,1)$ 为椭圆.
(其中$\theta$为截面$A_1C_1D$与圆锥的对称轴$DD_1$的夹角,$\alpha$为圆锥母线与圆锥对称轴的夹角)