[MCM] 多目标优化 MOP(multi-objective programming)

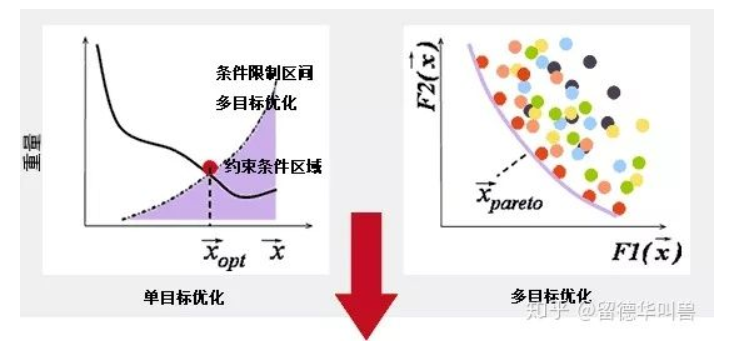
生活中许多问题都是由相互冲突和影响的多个目标组成。人们会经常遇到使多个目标在给定区域同时尽可能最佳的优化问题，也就是多目标优化问题。优化问题存在的优化目标超过一个并需要同时处理就成为多目标优化问题。

多目标优化问题在工程应用等现实生活中非常普遍并且处于非常重要的地位，这些实际问题通常非常复杂、困难，是主要研究领域之一。自20世纪60年代早期以来多目标优化问题吸弓了越来越多不同背景研究人员的注意力。因此，解决多目标优化问题具有非常重要的科研价值和实际意义。

实际中优化问题大多数是多目标优化问题，一般情况下，多目标优化问题的各个子目标之间是矛盾的，一个子目标的改善有可能会引起另一个或者另几个子目标的性能降低，也就是要同时使多个子目标一起达到最优值是不可能的，而只能在它们中间进行协调和折中处理，使各个子目标都尽可能地达到最优化。其与单目标优化问题的本质区别在于，它的解并非唯一，而是存在一组由众多Pareto最优解组成的最优解集合，集合中的各个元素称为Pareto最优解或非劣最优解。

一般地，多目标规划问题（multi-objective programming,MOP）可以描述成如下形式：

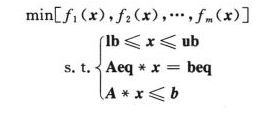
在两个目标函数中，它们之间可能是存在着一定的矛盾，也就是说，当一个目标函数的提高需要以另外一个目标函数的降低作为代价。在这个时候，我们就称，这样的两个解是非劣解，也就是长说的Pareto最优解。多目标优化算法就是要找到这些Pareto最优解。

简单的解决形式

一般采用两个目标函数加权相加的形式。加权可以解决两个目标函数量纲不一致，或者变化剧烈程度不一致的问题，不过权重本身需要人为选取。

一般不使用乘法来组合目标函数，因为这样会使得导数的形式变得复杂。

方法一

MOEA/D  单目标转换法

他的思想是基于分解的方法，把一个多目标优化问题转成一组单目标的问题，然后同时求解这一组问题，从而得出一组解。

当然他这个方法还有一部分是关于结合进化算法的，这里不展开，只提他的分解的思想。
具体的方法是把多目标每一个子目标归一化，然后给每个目标赋予一个权值，然后通过不断调整这些权值，从而获得一组不同权值的单目标问题，然后再去同时解决这一组问题。

比如只考虑2个目标，那么权值可以划分成（1,0），（0.9,0.1），。。。，（0,1）这样一组问题，然后依次往后求解。

方法二  绘制出pareto curve

无非就是目标函数加权或者绘制出pareto curve。可以证明的是每个选定参数加权目标函数得到的解其实都是在pareto curve上面的。不过在目标函数很多的时候，其实得到pareto curve是不太现实的，计算量略大。而且并不是解越多就越好。

我之前的应用是用来做决策支持的，所以求解过程不求得到全部的解，但是我需要得到的每一个解差异足够大，这样我在取舍的时候相对容易一些。基于此，在得到第一个解(加权目标函数)之后，把这个解重新加回到原问题里面，要求新的解跟已有解的差异最大化，以此类推。我可以在任何时候停止这个算法，但是可以确保我得到的几个解差异是足够大的。实际应用中，这样计算量大大减少，解之间的差异也足够大。如果需要话pareto curve，就多拿几个解，对pareto curve的全貌也有个大概理解了。

 

 

 

实例

NSGA-II 算法实例

目前的多目标优化算法有很多, Kalyanmoy Deb的带精英策略的快速非支配排序遗传算法(NSGA-II) 无疑是其中应用最为广泛也是最为成功的一种

gamultiobj，该函数是基于NSGA-II改进的一种多目标优化算法

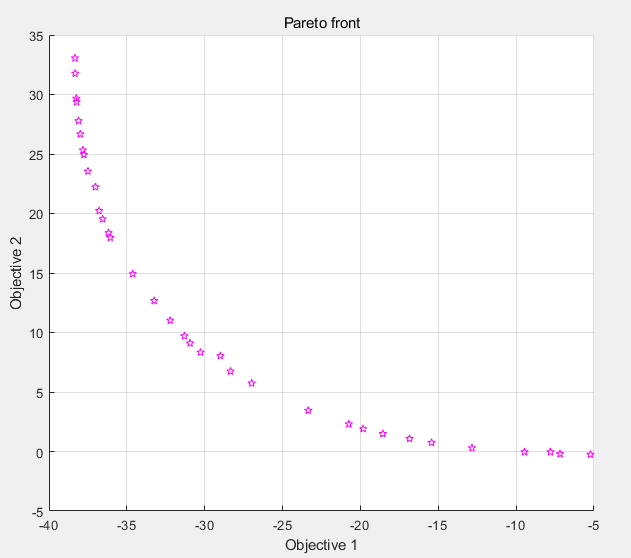
从图1可以看出Pareto前分布较均匀，多样性较好。