UVA1533-Moving Pegs（BFS+状态压缩）

Problem UVA1533-Moving Pegs

Accept：106  Submit：375

Time Limit: 3000 mSec

 Problem Description

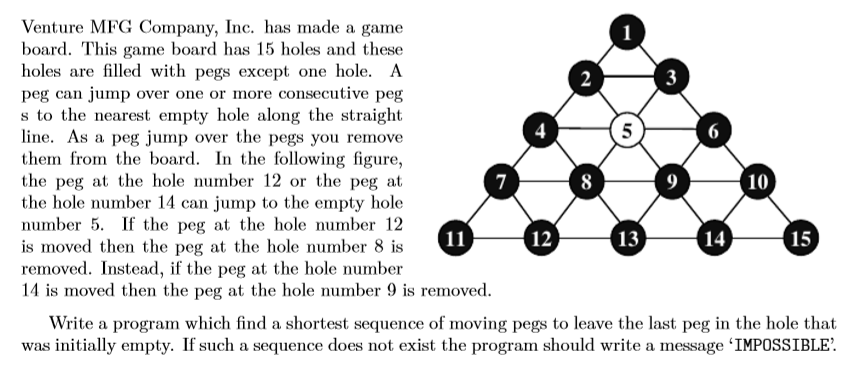
 Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case is a single integer which means an empty hole number.

 Output

For each test case, the first line of the output file contains an integer which is the number of jumps in a shortest sequence of moving pegs. In the second line of the output file, print a sequence of peg movements. Apegmovementconsistsofapairofintegersseparatedbyaspace. Thefirstintegerofthe pair denotes the hole number of the peg that is moving, and the second integer denotes a destination (empty) hole number.

 Sample Input

1

5

 

 

 Sample Ouput

10

12 5 3 8 15 12 6 13 7 9 1 7 10 8 7 9 11 14 14 5

题解：15个洞，二进制存储状态是比较正的思路。接下来就是水题了，只不过是把矩形地图换成了三角形地图，预处理一个临接表，存一下对于每个点能到哪些点。因为要字典序，因此顺序很重要，稍加分析就知道周围6个位置的大小关系，注意对于15个记录相邻点的数组，一定要统一顺序，除了字典序，还因为有可能要顺着一个方向走几格，这时顺序一致就很方便。

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = , maxm = ;
 const int dir[maxn][maxm] =
 {
     {-,-,-,-, , },  {-, ,-, , , },  { ,-, ,-, , },  {-, ,-, , , },
     { , , , , , },  { ,-, ,-, , },  {-, ,-, ,,},  { , , , ,,},
     { , , , ,,},  { ,-, ,-,,},  {-, ,-,,-,-},  { , ,,,-,-},
     { , ,,,-,-},  { , ,,,-,-},  { ,-,,-,-,-}
 };

 int s;
 bool vis[ << maxn];
 pair<int, int> path[ << maxn];
 int pre[ << maxn];

 struct Node {
     int sit, time;
     int pos;
     Node(int sit = , int time = , int pos = ) :
         sit(sit), time(time), pos(pos) {}
 };

 int bfs(int &p) {
     int cnt = ;
     int ori = ( << maxn) - ;
     ori ^= ( << s);
     queue<Node> que;
     que.push(Node(ori, , ));
     vis[ori] = true;
     while (!que.empty()) {
         Node first = que.front();
         que.pop();
         if (first.sit == ( << s)) {
             p = first.pos;
             return first.time;
         }

         int ssit = first.sit;
         for (int i = ; i < maxn; i++) {
             if (!(ssit&( << i))) continue;

             for (int j = ; j < maxm; j++) {
                 int Next = dir[i][j];
                 if (Next == - || !(ssit&( << Next))) continue;

                 int tmp = ssit ^ ( << i);
                 while (Next != -) {
                     if (!(ssit&( << Next))) {
                         //printf("%d %d\n",i, Next);
                         tmp ^= ( << Next);
                         if (!vis[tmp]) {
                             Node temp(tmp, first.time + , ++cnt);
                             pre[cnt] = first.pos;
                             path[cnt] = make_pair(i, Next);
                             que.push(temp);
                             vis[tmp] = true;
                         }
                         break;
                     }
                     tmp ^= ( << Next);
                     Next = dir[Next][j];
                 }
             }
         }
     }
     return -;
 }

 void output(int pos) {
     if (!pre[pos]) {
         printf("%d %d", path[pos].first + , path[pos].second + );
         return;
     }
     output(pre[pos]);
     printf(" %d %d", path[pos].first + , path[pos].second + );
 }

 int main()
 {
     int iCase;
     scanf("%d", &iCase);
     while (iCase--) {
         scanf("%d", &s);
         s--;
         memset(vis, false, sizeof(vis));
         memset(pre, -, sizeof(pre));
         int pos;
         int ans = bfs(pos);
         if (ans == -) {
             printf("IMPOSSIBLE\n");
         }
         else {
             printf("%d\n", ans);
             output(pos);
             printf("\n");
         }
     }
     return ;
 }