python数据结构与算法第十五天【二叉树】

1.树的特点

（1）每个节点有零个或多个子节点；

（2）没有父节点的节点称为根节点；

（3）每一个非根节点有且只有一个父节点；

（4）除了根节点外，每个子节点可以分为多个不相交的子树；

2.树的种类

• 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
• 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
• 二叉树：每个节点最多含有两个子树的树称为二叉树；
  • 完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
  • 平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
  • 排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
• 霍夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
• B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。

3. 树的使用场景

（1）xml，html等，那么编写这些东西的解析器的时候，不可避免用到树
（2）路由协议就是使用了树的算法
（3）mysql数据库索引
（4）文件系统的目录结构
（5）所以很多经典的AI算法其实都是树搜索，此外机器学习中的decision tree也是树结构

4.二叉树的性质

性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

5.树的创建代码实现

class Node(object):
    """节点类"""
    def __init__(self, elem=-1, lchild=None, rchild=None):
        self.elem = elem
        self.lchild = lchild
        self.rchild = rchild

class Tree(object):
    """树类"""
    def __init__(self, root=None):
        self.root = root

    def add(self, elem):
        """为树添加节点"""
        node = Node(elem)
        #如果树是空的，则对根节点赋值
        if self.root == None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
            #对已有的节点进行层次遍历
            while queue:
                #弹出队列的第一个元素
                cur = queue.pop(0)
                if cur.lchild == None:
                    cur.lchild = node
                    return
                elif cur.rchild == None:
                    cur.rchild = node
                    return
                else:
                    #如果左右子树都不为空，加入队列继续判断
                    queue.append(cur.lchild)
                    queue.append(cur.rchild)

5.树的广度优先遍历

def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if root == None:
            return
        queue = []
        queue.append(root)
        while queue:
            node = queue.pop(0)
            print node.elem,
            if node.lchild != None:
                queue.append(node.lchild)
            if node.rchild != None:
                queue.append(node.rchild)

6.二叉树的深度优先遍历

（1）先序遍历，即 根-左-右

def preorder(self, root):
      """递归实现先序遍历"""
      if root == None:
          return
      print root.elem
      self.preorder(root.lchild)
      self.preorder(root.rchild)

（2）中序遍历，即 左-根-右

def inorder(self, root):
      """递归实现中序遍历"""
      if root == None:
          return
      self.inorder(root.lchild)
      print root.elem
      self.inorder(root.rchild)

（3）后序遍历，即 左-右-根

def postorder(self, root):
      """递归实现后续遍历"""
      if root == None:
          return
      self.postorder(root.lchild)
      self.postorder(root.rchild)
      print root.elem

7.深度优先遍历举例：

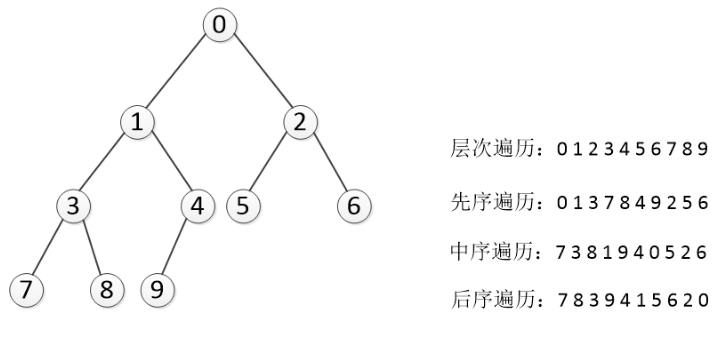
8.给出深度优先的先序和中序，请写出后序

自己实现