Leapin' Lizards

Leapin' Lizards

题目大意：

在一个网格地图中有一些高度不同的石柱，一些石柱上站着一些蜥蜴，你的任务是让尽量多的蜥蜴逃到边界外。 每行每列中相邻石柱的距离为1，蜥蜴的跳跃距离是d，即蜥蜴可以跳到平面距离不超过d的任何一个石柱上。石柱都不稳定，每次当蜥蜴跳跃时，所离开的石柱高 度减1（如果仍然落在地图内部，则到达的石柱高度不变），如果该石柱原来高度为1，则蜥蜴离开后消失。以后其他蜥蜴不能落脚。任何时刻不能有两只蜥蜴在同 一个石柱上。

这个应该还算是比较难的网络流的题目了吧， 至少对我这个刚刚接触新手的人来说只这样的，AC的过程是痛苦而又备受煎熬的，最后一步步调试下来成功提交的那刹那，感觉全身满满的正能量，闲话少扯了，下面开始直接讲我的思路。

一开始是从学长将网络流的ppt里面看到这题的，只知道是个最大流却又不知道怎么建图，然后想了一下，每根石柱上面能够供蜥蜴（包括一开始在它上面的蜥蜴）不会超过石柱的高

度，也就是可以把它的高度作为一个限制，这样把每一根石柱（i，j）（一维化表示为f = i*m+j)拆分为两个点u，v ，其中u= 2*f， v = 2*f+1，（也就是2*f^1),然后建立一条从

u--->v的边，容量为石柱高度。

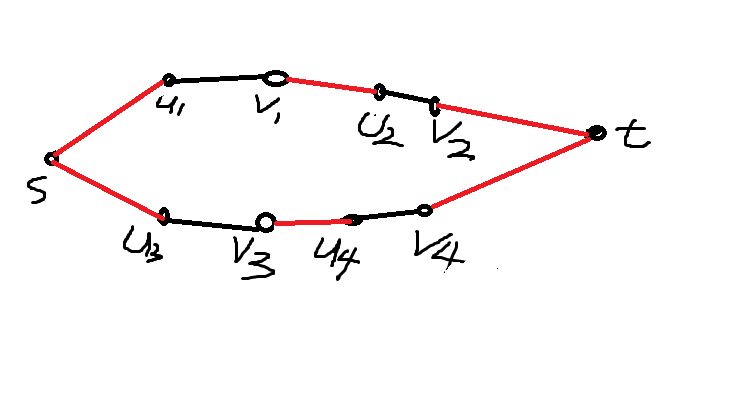
然后怎样表示各个石柱之间的到达关系呢？对于两根距离不超过d的石柱，也就是蜥蜴能够从一根跳到另一根的时候，例如石柱1,2，可以建立v1--->u2,的一条容量无限大的边，由于

可自由跳动，因此应该反向再建一条，即u2-->v1的边。   对于一开始上面就有蜥蜴的石柱，以及能够跳出边界的石柱，我是这样处理的：有蜥蜴的边，从起点s建立一条到该石柱

的拆分点u的边，容量为1，应该是单向的；然后对于能够跳出边界，即到达安全区域的石柱，建立一条从该石柱的拆分点v到汇点t的无穷容量的边。

然后利用ISPA算方法就可以了，初始可分配流量可以大胆的分配为inf，因为起点到每一个石柱（有蜥蜴）拆分点的容量限制为1，这样就可以表示该石柱上一开始有唯一的蜥蜴。

代码如下：

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <cstdlib>
  4 #include <queue>
  5 #include <algorithm>
  6 #include <cmath>
  7 #define esp 1e-6
  8 #define inf 0x0f0f0f0f
  9 #define INF 200000
 10 #define N 30
 11 using namespace std;
 12
 13 struct EDGE
 14 {
 15     int i, c;
 16     EDGE *next, *ani;
 17 } *Edge[INF], E[INF];
 18 int Dfn[INF], Now[INF], cnt, flag[INF];
 19 int src, sink;
 20 int n, m, d, tot, ndot;
 21 char aMat[N][N], bMat[N][N];
 22
 23 int dblcmp(double x)
 24 {
 25     if(fabs(x) < esp)
 26         return 0;
 27     return x > 0 ? 1 : -1;
 28 }//读图
 29 void ReadMat(int r, int &len, char (*Mat)[N])
 30 {
 31     for(int i = 0; i < r; i++)
 32         scanf("%s", Mat[i]);
 33     len = strlen(Mat[0]);
 34 }//返回石柱的高度
 35 int f(int i, int j)
 36 {
 37     return aMat[i][j] - '0';
 38 }//计算两根石柱之间的距离
 39 double cal(double x, double y)
 40 {
 41     return sqrt(x*x+y*y);
 42 }
 43 void add(int i, int j, int c, EDGE &e1, EDGE &e2)
 44 {
 45     e1.i = j, e1.c = c, e1.next = Edge[i], e1.ani = &e2, Edge[i] = &e1;
 46     e2.i = i, e2.c = 0, e2.next = Edge[j], e2.ani = &e1, Edge[j] = &e2;
 47 }
 48 void build(void)
 49 {
 50     for(int i = 0; i < n; i++)
 51         for(int j = 0; j < m; j++)
 52         {
 53             int u, v, c;
 54             if((c = f(i, j)))//表示该位置为石柱
 55             {//拆分点
 56                 u = 2*(i*m+j), v = u ^ 1;
                    //拆分点之间建立边
 57                 add(u, v, c, E[cnt], E[cnt + 1]);
 58                 cnt +=2;
 59                 add(v, u, c, E[cnt], E[cnt + 1]);
 60                 cnt += 2;
 61                 if(bMat[i][j] == 'L')//石柱上面有蜥蜴
 62                 {
 63                     tot++;
 64                     add(src, u, 1, E[cnt], E[cnt + 1]);//将源点和该有蜥蜴的石柱连接一条容量为1的边
 65                     cnt +=2;
 66                 }//搜索周围能够到达的石柱
 67                 for(int ii = i - d; ii <= i + d; ii++)
 68                     for(int jj = j - d; jj <= j + d; jj++)
 69                         if(!(ii == i && jj == j))
 70                         {
 71                             double dist = cal(ii - i, jj -j);
 72                             if(dblcmp(d - dist) >= 0)
 73                             {//石柱能够到达边界
 74                                 if((ii < 0 || ii >= n || jj < 0 || jj >= m ) )
 75                                 {
 76                                     if(!flag[v])
 77                                         add(v, sink, inf, E[cnt], E[cnt + 1]),
 78                                             flag[v] = 1,
 79                                                       cnt += 2;
 80                                 }//能够到达另一个石柱
 81                                 else if(f(ii, jj))
 82                                 {
 83                                     u = 2*(ii*m+jj);//两根石柱之间建立一条无穷容量的边
 84                                     add(v, u, inf, E[cnt], E[cnt + 1]);
 85                                     cnt += 2;
 86                                 }
 87                             }
 88                         }
 89             }
 90         }
 91 }
 92 void init(void)
 93 {
 94     memset(Edge, 0, sizeof(Edge));
 95     memset(flag, 0, sizeof(flag));
 96     cnt = tot = 0;
 97 }
 98
 99 int ISAP(int s, int end, int flow)
100 {
101     if(s == end)
102         return flow;
103     int i, tab = ndot -1, now = 0, vary;
104     for(EDGE *p = Edge[s]; p && flow - now; p = p->next)
105         if(p->c)
106         {
107             if(Dfn[s] == Dfn[i = p->i] + 1)
108                 vary = ISAP(i, end, min(flow - now, p->c)),
109                 p->c -= vary, p->ani->c += vary, now +=vary;
110             if(p->c)
111                 tab = min(tab, Dfn[i]);
112             if(Dfn[src] == ndot)
113                 return now;
114         }
115     if(now == 0)
116     {
117         if(--Now[Dfn[s]] == 0)
118             Dfn[src] = ndot;
119         Now[Dfn[s] = tab + 1]++;
120     }
121     return now;
122 }
123 int max_flow(int s, int end)
124 {
125     memset(Dfn, 0, sizeof(Dfn));
126     memset(Now, 0, sizeof(Now));
127     Now[0]  =  ndot;
128     int ret = 0;
129     for(; Dfn[s] < ndot;)
130     {
131
132         ret += ISAP(s, end, inf);
133     }
134     return ret;
135 }
136 int main(void)
137 {
138     int T;
139     for(int t = scanf("%d", &T); t <= T; t++)
140     {
141         init();
142         scanf("%d%d", &n, &d);
143         ReadMat(n, m, aMat);
144         ReadMat(n, m, bMat);
145         src = 2*n*m, sink = 2*n*m+1;
146         build();
147         ndot = sink + 1;
148         int ans = max_flow(src, sink);
149         ans = tot - ans;
150         if(ans)
151             printf("Case #%d: %d lizard%sleft behind.\n", t,ans,(ans == 1)?" was ":"s were ");
152         else printf("Case #%d: no lizard was left behind.\n", t);
153     }
154     return 0;
155 }

 

 

分类: ACM_日常总结, POJ, 图论, 最大流

标签: 拆点