JAVA中的数据结构 - 1，红黑树

背景：

在JDK源码中, 有treeMap和JDK8的HashMap都用到了红黑树去存储

红黑树可以看成B树的一种:

二叉树-->搜索二叉树-->平衡搜索二叉树-->B树--> 红黑树

故我提取出了红黑树部分的源码，去说明红黑树的理解

看之前，理解红黑树的几个特性，后面的操作都是为了让搜索二X树符合红黑树的这几个特性，从而满足对查找效率的O(logn)

红黑树特效

1，根和叶子节点都是黑色的

2，不能有有连续两个红色的节点

3， 从任一节点到它所能到达得叶子节点的所有简单路径都包含相同数目的黑色节点

这几个特效，个人理解就是规定了红黑树是一颗2-3-4的B树了，从而满足了O(logn)查找效率

改变方法，这些改变也都是在O(logn)内完成的

1， 改变颜色

2， 左旋

3， 右旋

从JDK源码来理解

先看TreeMap

//对treeMap的红黑树理解注解. 2017.02.16 by 何锦彬  JDK,1.7.51<br>  <br>/** From CLR */
    private void fixAfterInsertion(Entry<K, V> x) {

        //新加入红黑树的默认节点就是红色
        x.color = RED;
        /**
         * 1. 如为根节点直接跳出
         */
        while (x != null && x != root && x.parent.color == RED) {

            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {

                //如果X的父节点（P）是其父节点的父节点（G）的左节点
                //即 下面这种情况
                /**
                 *                         G
                 *               P(RED)              U
                 */
                //获取其叔(U)节点
                Entry<K, V> y = rightOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) {
                    // 这种情况
                    /**
                     *                         G
                     *               P(RED)              U(RED)
                     *          X
                     */
                    //如果叔节点是红色的（父节点有判断是红色）. 即是双红色，比较好办，通过改变颜色就行. 把P和U都设置成黑色然后,X加到P节点。 G节点当作新加入节点继续迭代
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {
                    //处理红父，黑叔的情况
                    if (x == rightOf(parentOf(x))) {
                        // 这种情况
                        /**
                         *                           G
                         *            P(RED)                        U(BLACK)
                         *                     X
                         */
                        //如果X是右边节点
                        x = parentOf(x);
                        // 进行左旋
                        rotateLeft(x);
                    }
                    //左旋后，是这种情况了
                    /**
                     *                           G
                     *            P(RED)                        U(BLACK)
                     *      X
                     */

                    // 到这，X只能是左节点了，而且P是红色，U是黑色的情况
                    //把P和G改成黑色，以G为节点进行右旋
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateRight(parentOf(parentOf(x)));
                }
            } else {
                //父节点在右边的
                /**
                 *                         G
                 *                 U               P(RED)
                 */
                //获取U
                Entry<K, V> y = leftOf(parentOf(parentOf(x)));

                if (colorOf(y) == RED) {
                    //红父红叔的情况
                    /**
                     *                          G
                     *             U(RED)               P(RED)
                     */
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    //把G当作新插入的节点继续进行迭代
                    x = parentOf(parentOf(x));
                } else {
                    //红父黑叔，并且是右父的情况
                    /**
                     *                          G
                     *             U(RED)               P(RED)
                     */
                    if (x == leftOf(parentOf(x))) {
                    //如果插入的X是左节点
                     /**
                        *                            G
                        *            U(BLACK)                        P(RED)
                        *                                       X
                        */
                        x = parentOf(x);
                        //以P为节点进行右旋
                        rotateRight(x);
                    }
                    //右旋后
                    /**
                     *                            G
                     *            U(BLACK)                        P(RED)
                     *                                                        X
                     */
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    //以G为节点进行左旋
                    rotateLeft(parentOf(parentOf(x)));
                }
            }
        }
        //红黑树的根节点始终是黑色
        root.color = BLACK;
    }

再看看HashMap的实现，

在HashMap中，在JDK8后开始用红黑树代替链表，查找由O(n) 变成了 O(Logn)

源码分析如下:

for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        //JDK8 的hashmap，链表到了8就需要变成颗红黑树了
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }

红黑树的维护代码部分如下：

//hashmap的红黑树平衡
         static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
                                                            TreeNode<K,V> x) {
                    x.red = true;
                    //死循环加变量定义，总感觉JAVA很少这样写代码 哈
                    for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
                        //xp X父节点， XPP X的祖父节点，  XPPL 祖父左节点  XXPR 祖父右节点
                        if ((xp = x.parent) == null) {
                            x.red = false;
                            return x;
                        }
                        // 如果父节点是黑色， 或者XP父节点是空，直接返回
                        else if (!xp.red || (xpp = xp.parent) == null)
                            return root;

                        // 下面的代码就和上面的很treeMap像了，

                        if (xp == (xppl = xpp.left)) {
                             // 第一种情况, 赋值xppl
                            //父节点是左节点的情况,下面这种
                            /**
                             *                         G
                             *               P(RED)              U
                             */
                            if ((xppr = xpp.right) != null && xppr.red) {
                                //如果红叔的情况
                                 // 这种情况
                                /**
                                 *                         G
                                 *               P(RED)              U(RED)
                                 *          X
                                 */
                                 //改变其颜色，
                                xppr.red = false;
                                xp.red = false;
                                xpp.red = true;
                                x = xpp;
                            }
                            else {
                                 // 黑叔的情况
                                //  这种情况
                              /**
                                 *                         G
                                 *               P(RED)              U(BLACK)
                                 */
                                if (x == xp.right) {
                                    //如果插入节点在右边 这种
                                     // 这种情况
                                    /**
                                     *                           G
                                     *            P(RED)                        U(BLACK)
                                     *                     X
                                     */
                                    //需要进行左旋
                                    root = rotateLeft(root, x = xp);
                                    xpp = (xp = x.parent) == null ? null : xp.parent;
                                }
                                //左旋后情况都是这种了
                                /**
                                 *                           G
                                 *            P(RED)                        U(BLACK)
                                 *      X
                                 */
                                // 到这，X只能是左节点了，而且P是红色，U是黑色的情况
                                if (xp != null) {
                                //把P和G改成黑色，以G为节点进行右旋
                                    xp.red = false;
                                    if (xpp != null) {
                                        xpp.red = true;
                                        root = rotateRight(root, xpp);
                                    }
                                }
                            }
                        }
                        else {
                             //父节点在右边的
                            /**
                             *                         G
                             *                 U               P(RED)
                             */
                            //获取U
                            if (xppl != null && xppl.red) {
                                //红父红叔的情况
                                 /**
                                 *                           G
                                 *                 U(RED)               P(RED)
                                 */
                                xppl.red = false;
                                xp.red = false;
                                xpp.red = true;
                                x = xpp;
                            }
                            else {

                                if (x == xp.left) {
                                    //如果插入的X是右节点
                                  /**
                                     *                            G
                                     *            U(BLACK)                        P(RED)
                                     *                                       X
                                     */
                                    root = rotateRight(root, x = xp);
                                    xpp = (xp = x.parent) == null ? null : xp.parent;
                                }
                                //右旋后
                                /**
                                 *                            G
                                 *            U(BLACK)                        P(RED)
                                 *                                                        X
                                 */
                                if (xp != null) {
                                    xp.red = false;
                                    if (xpp != null) {
                                        xpp.red = true;
                                        root = rotateLeft(root, xpp);
                                    }
                                }
                            }
                        }
                    }

可见，其实处理逻辑都一样：

流程图如下:

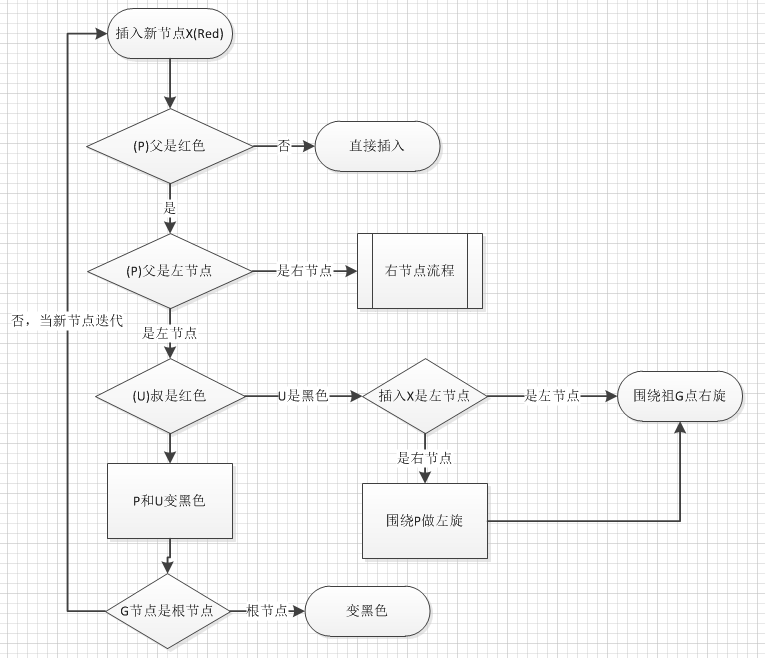
先谈谈我对红黑树的理解

一， 从2-3-4树去理解

红黑树，其实是一颗 2-3-4的B树，如果这样理解就能知道为什么能O（logn）的查找了

可以把红色节点看成是连接父节点的组成的一个大节点，如下:

红色的就是和父节点组成了

1， B+树都是从底布开始往上生长，自动平衡，如 2-3-4树，当节点达到了3个时晋升到上个节点，所以不会产生单独生长一边的情况，形成平衡。

2-3-4树和红黑树的对应

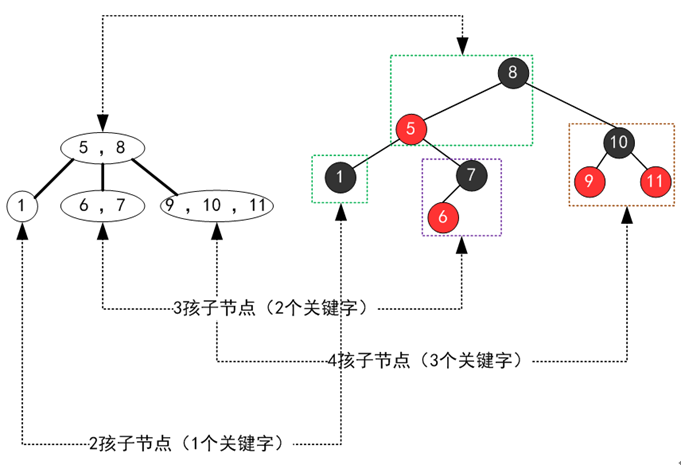
（此图转自网上）

红色节点可以看成为和父节点组成的链接，比如上图的9 10 11，9和11都是红色，看成是两边的链接。

因为红黑树是一颗2-3-4树，故能保持相对的平衡，从而保证了操作的O(LgN)

欢迎关注我的公众号，重现线上各种BUG， 一起来构建我们的知识体系