图的最小生成树(Prim、Kruskal)

理论：

Prim：

基本思想：假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

Prim算法的核心:始终保持TE中的边集构成一棵生成树。

Kruskal：

假设连通网N＝（V，{E}）。则令最小生成树的初始状态为只有n个顶点而无边的非连通图T＝（V，{}），图中每个顶点自成一个连通分量。

在E中选择最小代价的边，若该边依附的顶点落在T中不同的连通分量中，则将该边加入到T中，否则舍去此边而选择下一条代价最小的边，依次类推，直到T中所有顶点都在同一连通分量上为止。

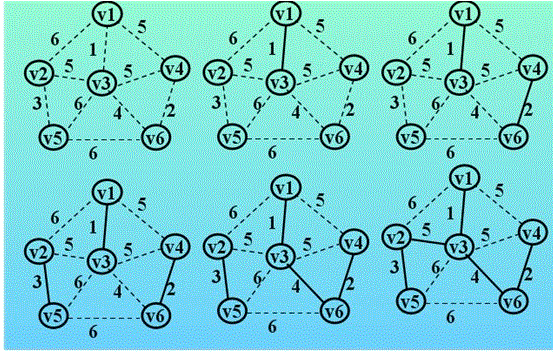
两者比较；

prim算法适合稠密图，其时间复杂度为O(n^2)，其时间复杂度与边得数目无关，而kruskal算法的时间复杂度为O(eloge)跟边的数目有关，适合稀疏图。

java实现

Vertex.java

package 图;

public class Vertex{
    String value;
    boolean isVisited;
    Vertex(String value)
    {
        this.value=value;
        this.isVisited=false;
    }
    public String getValue() {
        return value;
    }
    public void setValue(String value) {
        this.value = value;
    }
    public boolean isVisited() {
        return isVisited;
    }
    public void setVisited(boolean isVisited) {
        this.isVisited = isVisited;
    }

}

Edge.java

package 图;

public class Edge{
    Vertex start;
    Vertex end;
    int value;
    public Vertex getStart() {
        return start;
    }

    public void setStart(Vertex start) {
        this.start = start;
    }

    public Vertex getEnd() {
        return end;
    }

    public void setEnd(Vertex end) {
        this.end = end;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    Edge(Vertex start,Vertex end, int value){
        this.start=start;
        this.end=end;
        this.value=value;
    }
}

Graph.java

    package 图;

    import java.util.ArrayList;
    import java.util.Collections;
    import java.util.Comparator;
    import java.util.Iterator;
    import java.util.List;
    import java.util.Stack;

    public class Graph {

        public static List<Vertex> vertexList=new ArrayList<Vertex>();
        public static List<Edge> EdgeQueue=new ArrayList<Edge>();
        public static List<Vertex> newVertex=new ArrayList<Vertex>();
        public static List<Edge> newEdge=new ArrayList<Edge>();

        public static void buildGraph(){
            Vertex a=new Vertex("a");
            vertexList.add(a);
            Vertex b=new Vertex("b");
            vertexList.add(b);
            Vertex c=new Vertex("c");
            vertexList.add(c);
            Vertex d=new Vertex("d");
            vertexList.add(d);
            Vertex e=new Vertex("e");
            vertexList.add(e);
            Vertex f=new Vertex("f");
            vertexList.add(f);

            addEdge(a, b, 3);
            addEdge(a, e, 6);
            addEdge(a, f, 5);
            addEdge(b, a, 3);
            addEdge(b, c, 1);
            addEdge(b, f, 4);
            addEdge(c, b, 1);
            addEdge(c, d, 6);
            addEdge(c, f, 4);
            addEdge(d, c, 6);
            addEdge(d, f, 5);
            addEdge(d, e, 8);
            addEdge(e, d, 8);
            addEdge(e, f, 2);
            addEdge(e, a, 6);
            addEdge(f, a, 5);
            addEdge(f, b, 4);
            addEdge(f, c, 4);
            addEdge(f, d, 5);
            addEdge(f, e, 2);

        }

        public static void addEdge(Vertex start,Vertex end,int value){
            Edge e=new Edge(start,end,value);
            EdgeQueue.add(e);
        }
        public static boolean containVertex(Vertex v){

            for(Vertex each:newVertex)
            {
                if(each.value.equals(v.value))
                    return true;
            }
            return false;
        }

        public static void prim(){
            buildGraph();
            Vertex start=vertexList.get(0);
            newVertex.add(start);

            for(int i=0; i<vertexList.size(); i++)
            {
                Vertex temp=new Vertex(start.value);
                Edge tempEdge=new Edge(start, start, 1000);

                for(Vertex v:newVertex)
                {
                    for(Edge e:EdgeQueue)
                    {
                        if(e.start==v && !containVertex(e.end))
                        {
                            if(tempEdge.value>e.value)
                            {
                                tempEdge=e;
                                temp=e.end;
                            }
                        }
                    }
                }
                newVertex.add(temp);
            }

            Iterator<Vertex>i=newVertex.iterator();
            while(i.hasNext())
            {
                Vertex v=i.next();
                System.out.print(v.value+" ");
            }
        }

        public static void kruskal(){
            buildGraph();
            sort();
        }

        public static void sort(){
            Comparator<Edge>comparator=new Comparator<Edge>(){

                @Override
                public int compare(Edge e1, Edge e2) {
                    // TODO Auto-generated method stub
                    return e1.getValue()-e2.getValue();
                }
            };
            Collections.sort(EdgeQueue,comparator);
        }

        public static void main(String[] args) {
               prim();
        }
    }