2019清明期间qbxt培训qwq

• 4.4上午：数学基础

（qwq整成word和cpp了，它居然不能直接把文档附上来）

• part 1：高精度运算

高精加和高精减就不说了，之前写过博客了qwq，讲一讲高精乘和高精除吧。

1.高精度乘法（不知道为甚么害怕自己忘了老想再写一遍）：

题干（就很简单惹）：给定两个数a，b，求他们的乘积（a和b都很大）；

显然如果直接乘，用一个数组存的话，可能会爆掉，（_int128也会爆的qwq），这时或许可以考虑将每一位分开存，然后就引入了神奇的高精度：

先读入两个数：这里用的是字符串char读入然后把每一位数字存到数组中：

for(int i = lena-;i >= ;i--)a[lena-i] = a1[i]-;//把字符串存进数组中
for(int i = lenb-;i >= ;i--)b[lenb-i] = b1[i]-;
    /*刚刚搞了个大乌龙qwq（直接 a[lena-i] = a1[lena]-48;b[lenb-i] = b1[lenb]-48;*/
/*插入的主要代码qwq，lena，lenb分别为字符串a1，b1的长度。这里从1~len分别存从个位到x位的数字*/

首先有一个必须要解决的问题：乘出来的数应该存到哪一位？？不妨模拟一下乘法计算：

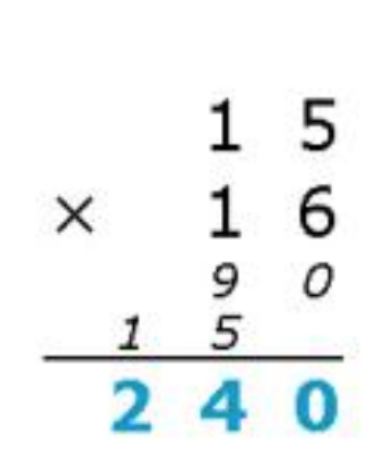由此可以看出，第一个数的第i项*第二个数的第j项应该放在i+j-1的位置。

搞定了前面，就可以进行乘法运算惹.，真的吹爆lh的算法：lh是先乘起来再处理，赶脚这样更好想也更好些一点；而且lh也没有用什么特判if之类的，让我这个蒟阵非常清楚自己在干什么qwq，比某ybt好多惹。

代码惹：

for(int i = ;i <= lena;i++)
      for(int j = ;j <= lenb;j++)
        c[i+j-] = c[i+j-]+a[i]*b[j]; //进行乘法运算
    int len=lena+lenb-;//暂时定义最后答案的长度为lena+lenb-1（或许会更长，一会再处理）
    for(int i=;i<=len;i++){
        c[i+]+=c[i]/;//又搞了个乌龙导致答案算错惹，这些大概都是我的弱点吧（写一遍错一遍qwq
        c[i]%=;
    }

进行收尾的数据处理：

显然乘法计算时可能会有超出lena+lenb-1的情况，所以我们或许大概（啊呸）（那得麻溜的处理啊）需要处理一下：

这里有一个小细节，处理前方非零数位时，要用while而不是if,因为前面的数可能有若干个（突然想不没明白了qwq）

好惹，上代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
char a1[],b1[];
int a[],b[],c[],lena,lenb,lenc;
int main()
{
    scanf("%s",a1);
    lena = strlen(a1);
    scanf("%s",b1);
    lenb = strlen(b1);
    for(int i = lena-;i >= ;i--)a[lena-i] = a1[i]-;//把字符串存进数组中
    for(int i = lenb-;i >= ;i--)b[lenb-i] = b1[i]-;
    //刚刚搞了个大乌龙qwq（直接 a[lena-i] = a1[lena]-48;b[lenb-i] = b1[lenb]-48;
    for(int i = ;i <= lena;i++)
      for(int j = ;j <= lenb;j++){
        c[i+j-] += a[i]*b[j];
        } //进行乘法运算
    int len=lena+lenb-;//暂时定义最后答案的长度为lena+lenb-1（或许会更长，一会再处理）
    for(int i=;i<=len;i++){
        c[i+]+=c[i]/;
        c[i]%=;
    }
    while(c[len+]!=)len++;
    for(int i=len;i>=;i--)
    printf("%d",c[i]);
}//亲测15*3是对的qwq

2.高精度除法（这里只讲了高精/低精）：

其实高精除在乘法的基础上改一下核心语句就好惹，这里不细讲惹，我gun去写代码了，希望我核心的语句没有忘(写崩了写崩了！！！还是记不住qwq）:

找到了错误，感觉自己还是在小细节上不够仔细（buxianggenvsheng），像什么scanf没有加引执符，%d搞成%s（这个是输入字符数组b的时候忘记改过来了qwq）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

char a1[];
int a[],b,c[],lena;
int main()
{
    scanf("%s",a1);
    lena = strlen(a1);
    scanf("%d",&b);
    for(int i = lena-;i >= ;i--)a[lena-i] = a1[i]-;//把字符串存进数组中
    for(int i = lena;i >=;i--){//除法是唯一一个从高位开始算的
        c[i]=a[i]/b;
        a[i-1]+=(a[i]%b)*10;//意思是把这一位/b余下的余数加到下一位（比这一位低一位的）去（加到下一位就*10了呀）
    }
    while(c[lena]==)lena--;
    for(int i=lena;i>=;i--)
    printf("%d",c[i]);
}//亲测200/5有效

负数肿么办？？？

加法：一个数是负数：变为减法      两个数是负数：全部变为正数算加法，最后取负

减法：被减数是负数：全部变为正数算加法，最后取负    减数是负数：减数取负，变为加法    都是负数：都取负，变为减法，即（-减数）-（-被减数）

乘法：统计负数个数s 都变为非负数计算，若s为奇数，最后取负

• part2：模意义下的运算：

1.性质：

无除法运算，满足基本的交换律、分配率、结合律 对中间结果取模不影响最终答案

eg：快速幂

计算a^b % p = ?

法一：分治思想：

这个题洛谷有板子（不过编译失败是个什么鬼？？）（交了个板子题结果我炸了？？？）：

行吧经过我无数次（5次欸qwq）的没过板子emm我终于搞了个a了的代码：

分治的思想就是一分为二嘛，求a^b%p，可以先求a^（b/2）%p再相乘，然后再%p，要注意的是b不整除2的时候最后还要乘一个a，然后存答案的话要用long long，要不然会爆的（我就爆了***）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int a,b,p;
int fz(int a,int b,int p){
    long long ans=;
    if(b==)return ;//当b=0时，a^0=1；
    ans=fz(a,b/,p);//搞分治，b每次/2
    ans=ans*ans%p;
    if(b%==)
    ans=ans*a%p;//乘回来b为奇数的那个a
    return ans;
}
int main(){
    scanf("%d%d%d",&a,&b,&p);
    cout<<a<<"^"<<b<<" mod "<<p<<"=";//这个是洛谷板子题的要求qwq
    cout<<fz(a,b,p)%p<<endl;//一定要模p啊qwq
}

法二：快速幂（板子又没过emm难到我数据又爆了？？好像还真是qwq ）：

行惹过了。突然想小反思一下：

感觉自己学信息奥赛这么久了，总是犯一些细节性的东西，基础还是不扎实，还需要努力盘一盘基础qwq

快速幂思想算是比较难理解代码的思想了，其实数学思想还好，比较好理解，就怕代码qwq

下面是某只zay的lh的解释？？

a^7 = a^1 * a^2 * a^4   2进制：111

a^11 = a^1 * a^2 * a^8  2进制：1011

a^25 = a^1 * a^8 * a^16  2进制：11001

所以首先计算出 a^1、 a^2、 a^4、 a^8 …，利用2进制表示出a，若第x位上为1，则乘a的x次方，若为0，则不乘。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
long long a,b,p;
int kuaisumi(long long a,long long b,long long p){//钟大佬kuaisumi（拼音）的操作天下无敌了
    long long ans=;
    while(b>){
        if(b&)ans=ans*a%p;//满足第x位上是1，ans乘上a^（2^(x-1))；
        a=a*a%p;//这里一直计算着a^2k次方2k=2^(x-1);
        b/=;
    }
    return ans;
}
int main(){
    scanf("%d%d%d",&a,&b,&p);
    cout<<a<<"^"<<b<<" mod "<<p<<"=";
    cout<<kuaisumi(a,b,p)%p<<endl;
}

费马小定理：

对于素数p和任意正整数a(0 ~ p-1)，有a^(p-1) ≡ 1(mod p)

b * a = t

t * a^(p-2) = b t/a=b

//在模p意义下除以一个数等于乘这个数的p-2次方

应用：计算C(n,m) % (10^9+7)  10^9+7是质数  n ,m<=10,0000   Query 10,0000

思路：C(n, m) = n! / ( (n-m)! * m! )

= n! * ( (n-m)! * m! )^(p-2)

= n! * ( (n-m)! )^(p-2) * (m! )^(p-2) 预处理任意n！、(n! )^(p-2)

这个预处理怕不是要炸掉？？？（顺便吐槽下lh的代码质量qwq真的是金牌吗？？

日常写标程写炸qwq

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
long long n,m;
long long  b[],d[];
long long p=1e9+;
long long pow(long long a,long long b,long long p){//快速幂求阶乘的p-2次方
    long long ans=;
    while(b>){
        if(b&)ans=ans*a%p;
        a=a*a%p;
        b/=;
    }
    return ans;
}
long long C(long long x,long long y){//求组合数的函数（思路见上
    if(m>n)return -;
    if(m==n||m==)return ;
    else return b[x]*d[x-y]%p*d[y]%p;
}
int main(){
    scanf("%lld%lld",&n,&m);
    b[]=;
    for(int i=;i<=;i++)b[i]=b[i-]*i%p;//预处理1~100000的阶乘
    for(int i=;i<=;i++)d[i]=pow(b[i],p-,p)%p;//预处理1~100000阶乘的p-2次方

cout<<C(n,m)<<endl; }

拓展：给定n,m,p求C_n^m%p的值：

只需要改一下输入就可以了，变为输入三个数，p不再定义为1e9+7;

• part3：

1.最大公约数：

这里用到了辗转相除（mo）法：请自行百度：

代码qwq：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int a,b,x,y;
int gcd(int a,int b){
    if(b==)return a;
    else return gcd(b,a%b);
}
int main(){
    cin>>a>>b;
    cout<<gcd(a,b);
}

最小公倍数：

这里有个小知识qwq：

lcm（a，b）*gcd（a，b）=a*b；

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int a,b,x,y;
int gcd(int a,int b){
    if(b==)return a;
    else return gcd(b,a%b);
}
int main(){
    cin>>a>>b;
    cout<<a/gcd(a,b)*b;
}

end-