RE:从零开始的莫比乌斯反演

炫酷反演魔术根本看不懂啊。。。也就看看PoPoQQQ的ppt了。

这个赛季结束了，一年可以学很多很多东西呢。

因为我是写给自己看的所以写的很垃圾。

公式：

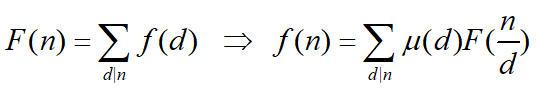
按我的理解，反演就是  x可以表示成y，然后我们想得到一个 y关于x的表达式。

所以形式就是 上面这个样纸。

叫做莫比乌斯函数，关于莫比乌斯函数有如下结论，

1. d=1,ud=1;

2.d=p1p2p3p4p5.....pk,  其中pi为互异的质数，那么 ud = (-1)^k;

3. 其他情况 u=0；

同时还有这么一个性质：

证明： n=1时显然，

n!=1时，根据唯一分解定理，

在n 的所有因子中，u值不为0的只有所有质因子次数为1的因子，其中质因数个数为r的因子数有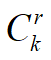个，

所以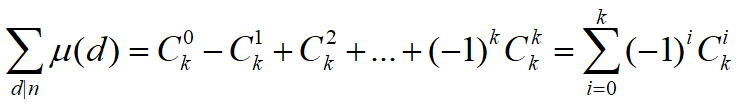

由二项式定理，令x=-1,y=1,代入即可证。

第二个性质：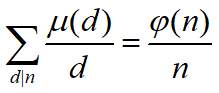

那个 φn就是欧拉函数，

欧拉函数的定义(来源 百度百科)：在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目,其中 φ1=1；

先给出一些欧拉函数的性质：来源：https://blog.csdn.net/YxuanwKeith/article/details/52387873

1.对于一个质数n，φn=n-1；证明：n是质数。(哈哈哈哈为什么我好想笑啊

2.若n=p^k，φn=p^k-p^(k-1);  证明：除了p的倍数其他数都与m互质。

3.就是辣个 结果公式，，我不会打字额

4.完了我死了我不会证明